Турнір вихідного дня 24-02
Бали: 100
Є прямокутний трикутник ~ABC~, кут ~ABC~ - прямий.
Відомі сторони ~|AB|~, ~|BC|~, ~|CA|~. Знайдіть площу цього трикутника.
Гарантується, що площа буде цілим числом.
Input
Вхідний потік містить три цілі числа ~|AB|~, ~|BC|~, ~|CA|~ (~1 \le |AB|, |BC|, |CA| \le 100~), які розділяються пропуском.
Output
У вихідний потік вивести площу трикутника.
Sample Input 1
3 4 5
Sample Output 1
6
Sample Input 2
5 12 13
Sample Output 2
30
Sample Input 3
45 28 53
Sample Output 3
630
Notes
До прикладу 1:
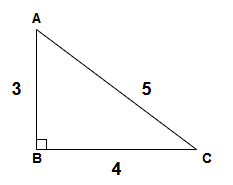
Бали: 100
Побудувати рамку 'зірочками' розмірності ~r \times c~
Input
Перший рядок містить ціле число ~T~ (~1 \le T \le 100~)- кількість тестів.
Наступні ~T~ рядків містять тести: два цілі числа ~r,c~ (~1 \le r,c \le 100~)
Output
Для кожного тесту вивести відповідно йому рамку. Тести розділяти порожнім рядком.
Sample Input 1
3
3 1
4 4
2 5
Sample Output 1
*
*
*
****
*..*
*..*
****
*****
*****
Бали: 100
Від станції ~A~ до станції ~B~ курсує потяг, проїзд на якому коштує ~X~ гривень. Крім того, від станції ~B~ до станції ~C~ курсує автобус, проїзд на якому коштує ~Y~ гривень. Степан купив для себе спеціальний квиток. З цим квитком він може сісти на автобус за половину вартості проїзду, якщо він їде від станції ~A~ до станції ~B~ на поїзді, а потім від станції ~B~ до станції ~C~ на автобусі.
Скільки коштує проїзд від станції ~A~ до станції ~C~ для Степана за спеціальним квитком?
Input
Вхідний потік містить два цілі числа ~X,Y~ (~1 \le X,Y \le 100~, Y - парне), які розділяються пропуском.
Output
Вивести вартість проїзду за спеціальним квитком від пункту ~A~ до пункту ~C~
Sample Input 1
81 58
Sample Output 1
110
Sample Input 2
4 54
Sample Output 2
31
Notes
Для прикладу 1:
Вартість проїзду на поїзді становить 81 гривень. Вартість проїзду на автобусі буде 58/2=29 гривень - знижка 50 відсотків.
Таким чином, проїзд від станції ~A~ до станції ~C~ коштує 110 гривень.
Бали: 100
При поділі ядра атома ядро розпадається на більше ніж одне ядро. На початку експерименту є N ядер. Починаючи з цього моменту (~t=0~), через кожну секунду кожне ядро буде розпадатися на ~K~ ядер. Не можна допустити щоб кількість ядер перевищувала ~M~ і тому треба зупинити реакцію поділу в якийсь момент часу ~t=T~.
Знайдіть значення ~T~.
Input
Вхідний потік містить три цілі числа ~N,K,M~ (~2 \le N,K,M \le 10^{18}~), які розділяються пропуском.
Output
У вихідний потік вивести значення ~T~.
Sample Input 1
2 2 7
Sample Output 1
1
Sample Input 2
2 2 8
Sample Output 2
2
Notes
Для прикладу 1:
при ~t=1~, кількість ядер дорівнює 4
при ~t=2~ кількість ядер буде 8.
Тому реакцію потрібно зупинити при t=1.