Тренування до ІІ етапу олімпіади з інформатики
Бали: 100
Прямокутник, із сторонами паралельними осям координат, заданий координатами протилежних сторін: (~X_1,Y_1~) та (~X_2,Y_2~).
Знайдіть площу прямокутника.
Обмеження
- ~0 \le X_1, Y_1, X_2, Y_2 \le 100~
Input
Перший рядок вхідного потоку містить цілі числа ~X_1, Y_1~.
Наступний рядок містить цілі числа ~X_2, Y_2~.
Числа у рядках розділяються пропуском.
Output
У вихідний потік вивести відповідь.
Sample Input 1
0 0
10 10
Sample Output 1
100
Sample Input 2
10 0
0 10
Sample Output 2
100
Бали: 100
Задається рядок ~S~ довжиною ~N~. Рядок ~S~ містить малі та великі літери англійського алфавіту.
Знайдіть кількість великих літер, які містяться в рядку ~S~.
Обмеження
- ~1 \le N \le 100~
- ~S~ містить лише малі та великі літери англійського алфавіту
Input
Перший рядок вхідного потоку містить ціле число ~N~.
Наступний рядок містить ~S~.
Output
У вихідний потік вивести відповідь.
Sample Input 1
3
AbC
Sample Output 1
2
Sample Input 2
3
abc
Sample Output 2
0
Бали: 100
На координатній площині задано ~N~ точок з цілими координатами (~X_i,Y_i~), де ~1 \le i \le N~.
Знайдіть порядковий номер точки з найбільшою абсцисою та найбільшою ординатою.
Якщо таких точок є декілька, то виведіть найменший порядковий номер.
Обмеження
~1 \le N \le 10^5~
~-10^6 \le X_i, Y_i \le 10^6~
Input
Перший рядок вхідного потоку містить ціле число ~N~.
Наступні ~N~ рядків містять цілі числа ~X_i, Y_i~. Числа розділяються пропуском.
Output
У першому рядку вихідного потоку вивести порядковий номер точки з максимальною абсцисою, а в другому - з мексимальною ординатою.
Sample Input 1
4
0 0
1 1
-1 10
5 -10
Sample Output 1
4
3
Sample Input 2
5
10 10
0 10
20 0
15 10
20 0
Sample Output 2
3
1
Бали: 100
Задається відсортований масив ~A~, який містить ~N~ цілих чисел та ціле число ~K~.
Ваше завдання знайти позицію(індекс) числа ~K~ в масиві ~A~. Відлік елементів починається з 0. Якщо число ~K~ відсутнє в масиві ~A~, то виведіть -1.
Обмеження
- ~1 \le N \le 10^5~
- ~1 \le A_i \le 10^6~
- ~1 \le K \le 10^6~
Input
Перший рядок вхідного потоку містить цілі числа ~N, K~.
Наступний рядок містить ~N~ цілих чисел ~A_i~.
Output
У вихідний потік вивести відповідь.
Sample Input 1
5 4
1 2 3 4 5
Sample Output 1
3
Sample Input 2
5 445
11 22 33 44 55
Sample Output 2
-1
Бали: 100
Степан та його друзі грають у гру з водяними рушницями. Гравці поділилися на дві команди: перша команда має номери від 1 до 4, а друга - від 5 до 8.
Сьогодні Степан судить гру. За кожне влучання гравця команда отримує 100 балів. Якщо на протязі 10 с фіксується ще одне влучання цього ж гравця, то додатково нараховується 50 балів для його команди.
Степан ретельно записав час та влучні постріли обох команд і має проблему із підрахунком балів.
Допоможіть Степану порахувати бали команд.
Обмеження
- ~1 \le n \le 100~
- ~0 \le t_i \le 1000~
- ~1 \le a_i , b_i \le 8~
Input
Перший рядок містить ціле число ~n~ - кількість пострілів, які відбулися під час гри.
Кожен із наступних ~n~ рядків містить три цілі числа ~t_i , a_i , b_i~ - гравець ~a_i~ влучив в гравця ~b_i~ в момент часу ~t_i~ (у секундах).
Гравці ~a_i~ та ~b_i~ гарантовано належать до різних команд.
Проміжки часу ~t_i~ є різними і впорядкованими за зростанням.
Output
Єдиний рядок має містити два числа, які розділеня пропуском: загальний бал першої команди і загальний бал другої команди.
Sample Input 1
3
10 1 6
20 1 7
21 8 1
Sample Output 1
250 100
Sample Input 2
3
10 2 5
15 2 6
25 2 5
Sample Output 2
400 0
Sample Input 3
2
10 5 2
11 6 3
Sample Output 3
0 200
Бали: 100
Дано рядок ~S~, який містить малі англійські символи.
Ваше завдання — написати програму для видалення мінімальної кількості таких символів із рядка ~S~, щоб рядок став паліндромом. Порядок символів змінювати не дозволяється.
Обмеження
- ~1 \le |S| \le 10^3~, де ~|S|~ - довжина рядка
- ~S~ містить символи проміжку ['a'..'z']
Input
Вхідний потік містить рядок ~S~.
Output
У вихідний потік вивести відповідь - мінімальну кількість символів, які треба видалити з рядка ~S~ щоб утворився паліндром.
Sample Input 1
aebcbda
Sample Output 1
2
Sample Input 2
abbsa
Sample Output 2
1
Бали: 100
~L~-кінь(~a,b~) може переміститися з клітинки (~x_1,y_1~) в клітинку (~x_2,y_2~) якщо виконуються одна із вимог:
~x_2=x_1 \pm a~ і ~y_2=y_1 \pm b~
або
~x_2=x_1 \pm b~ і ~y_2=y_1 \pm a~
Наприклад, ~L~-кінь(1,2) або ~L~-кінь(2,1) з червоної клітинки може переміститися в будь-яку зелену.
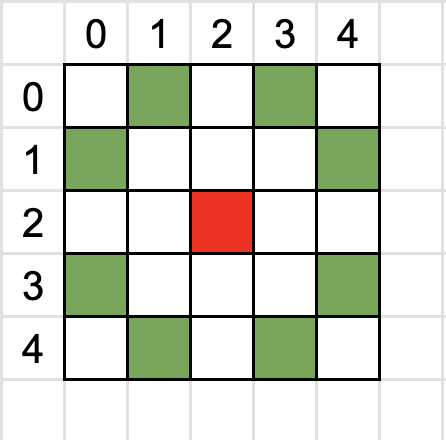
Дана шахівниця розміром ~n \times n~. Дайте відповідь на запитання для кожної пари (~a,b~), де ~1 \le a,b \le n~:
- Яка мінімальна кількість ходів потрібна для ~L~-кінь(~a,b~), щоб перейти з позиції (0,0) в позицію (n-1,n-1)? Якщо кінь не може дістатися до місця призначення, то виведіть -1.
Відповідь вивести для кожного ~L~-кінь(~a,b~) згідно формату вихідних даних.
Обмеження
- ~5 \le n \le 25~
Input
Вхідний потік містить одне ціле число ~n~ - розмірність шахівниці.
Output
У вихідний потік вивести ~n-1~ рядок. ~i~-й (де ~1 \le i \le n~) рядок містить ~n-1~ цілих чисел, розділених пропуском, які є мінімальною кількістю ходів для ~L~-кінь(~i,j~) для відповідного ~j~ (де ~1 \le j \le n~) щоб перейти з позиції (0,0) в позицію (n-1,n-1).
Наприклад, для ~n=3~ вихідні дані для всіх пар (~i,j~) розтащуються таким чином:
(1,1) (1,2)
(2,1) (2,2)
Sample Input 1
5
Sample Output 1
4 4 2 8
4 2 4 4
2 4 -1 -1
8 4 -1 1
Notes
Приклади можливих ходів для різних ~(i,j)~:
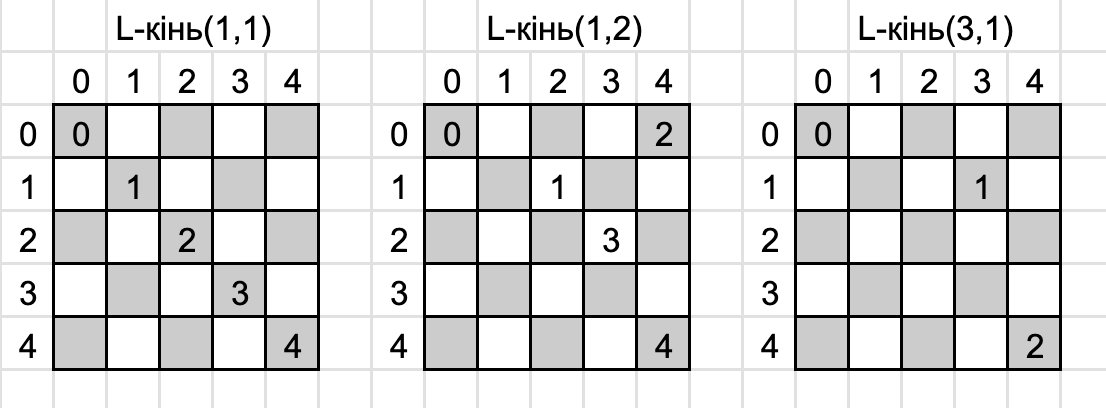
Бали: 100
Існує неорієнтований граф з ~N~ вершинами, пронумерованими від 1 до ~N~, кількість ребер на початку рівна 0.
Обробіть ~Q~ запитів у порядку їх слідування. Після обробки кожного запиту виведіть кількість вершин, які не з'єднані ребром з іншими вершинами.
~I~-й запит ~q_i~ належить до одного з двох наступних типів:
– 1 ~u~ ~v~: з'єднати вершину ~u~ і вершину ~v~ ребром. Гарантується, що коли задається цей запит, вершина ~u~ та вершина ~v~ не з'єднані ребром.
– 2 ~v~: видаліть усі ребра, які з'єднують вершину ~v~ та інші вершини. (Сама вершина ~v~ не видаляється.)
Обмеження
- ~2 \le N \le 3 \cdot 10^5~
- ~1 \le Q \le 3 \cdot 10^5~
- Для кожного запиту першого типу ~1 \le u,v \le N~ і ~u \neq v~.
- Для кожного запиту другого типу ~1 \le v \le N~.
- Безпосередньо перед подачею запиту першого типу між вершинами ~u~ і ~v~ немає ребра.
- Усі значення у вхідних даних є цілими числами.
Input
Перший рядок вхідного потоку містить цілі числа ~N, Q~.
Наступні ~Q~ рядків містять запити ~q_i~.
Output
У вихідний потік вивести ~Q~ рядків. В ~i~-му рядку ~(1 \le i \le Q)~ має бути записано кількість вершин, які не з'єднані ребром з іншими вершинами.
Приклад вхідних 1:
Після першого запиту вершина 1 і вершина 2 з'єднані одна з одною ребром, але вершина 3 не з'єднана з іншими вершинами. Таким чином, 1 виводимо в першому рядку.
Після третього запиту всі пари різних вершин з'єднуються ребром.
Четвертий запит просить видалити всі ребра, які з'єднують вершину 1 та інші вершини, зокрема, видалити ребро між вершиною 1 і вершиною 2, а також між вершиною 1 і вершиною 3. У результаті вершина 2 і вершина 3 з'єднані одна з одною, тоді як вершина 1 не з'єднана ребром з іншими вершинами. Таким чином, виводимо 0 і 1 в третьому і четвертому рядках відповідно.
Sample Input 1
3 7
1 1 2
1 1 3
1 2 3
2 1
1 1 2
2 2
1 1 2
Sample Output 1
1
0
0
1
0
3
1
Sample Input 2
2 1
2 1
Sample Output 2
2