Інтернет-олімпіада 2024, онлайн-тур
Бали: 100
До участі в олімпіаді з програмування допускаються тільки змішані команди з 3 учасників (1 хлопець і 2 дівчини або 1 дівчина і 2 хлопці). У школі ~N~ дівчат і ~M~ хлопчиків.
Напишіть програму, яка знаходить максимальну кількість команд, яку можуть сформувати учні даної школи.
Input
Перший рядок містить два цілих числа ~N~ і ~M~ (~1 \le N, M \le 10^{12}~) – кількість дівчат і кількість хлопчиків у школі.
Output
У першому рядку виведіть одне ціле число – максимальну кількість змішаних команд.
Sample Input 1
3 4
Sample Output 1
2
Sample Input 2
3 10
Sample Output 2
3
Notes
1. З 3 дівчат і 4 хлопців можна сформувати 2 змішані команди (1 дівчина + 2 хлопці) або (2 дівчини + 1 хлопець) і (1 дівчина + 2 хлопці).
2. З 3 дівчат і 10 хлопців можна сформувати 3 змішані команди (1 дівчина + 2 хлопці); 4 хлопці в змаганнях брати участь не будуть.
Бали: 100
На довгій стрічці одне за одним записані ~N~ цілих чисел – усі цілі числа від 1 до ~N~. Кожне з цих чисел записане рівно один раз і повторюваних чисел немає. Числа необов'язково писати в порядку зростання (від меншого до більшого). Між кожними двома числами є пробіл. Ми можемо розрізати стрічку там, де є пробіли. Мета полягає в тому, щоб, розрізавши стрічку, ми могли потім переставити шматки стрічки (не обертаючи їх) так, щоб в отриманій послідовності числа були розташовані в порядку зростання.
Напишіть програму, яка знаходить найменшу кількість розрізів, які ми можемо зробити, щоб розташувати отримані частини вказаним чином?
Input
Перший рядок містить одне ціле число ~N~ (~1 \le N \le 1 000 000~).
Наступні ~N~ рядків містять цілі числа - числа зі стрічки в тому порядку, в якому вони були записані на стрічку.
Output
Виведіть два цілі числа, розділені рівно одним пробілом: кількість зроблених розрізів і кількість чисел у найдовшій частині стрічки, отриманої в результаті розрізів.
Sample Input 1
12
12
1
2
4
5
6
7
10
11
3
8
9
Sample Output 1
5 4
Notes
Місце кожного розрізу позначається знаком |:
12 | 1 2 | 4 5 6 7 | 10 11 | 3 | 8 9
Найдовша частина стрічки після розрізів містить числа 4 5 6 7 і їх кількість 4.
Бали: 100
Леді розважається в системі координат. Починаючи з точки (0, 0), вона хоче досягти точки (~N,M~) рівно за ~K~ секунд. Кожної секунди Леді може збільшити свою координату ~x~ щонайбільше на ~A~, а ~y~-координату не більше ніж на ~B~. Формально, якщо Леді знаходиться в клітинці (~x, y~), вона може стрибнути за одну секунду в клітинку (~x', y'~), тільки якщо ~x \le x' \le x+A~ і ~y \le y' \le y+B~.
Напишіть програму, яка знаходить кількість способів, якими дівчина може досягти своєї мети. Зауважте, що протягом секунди Леді може вирішити не змінювати одну (або обидві) свої координати, але вона не може їх зменшити.
Оскільки відповідь може бути дуже великою - виведіть її за модулем 1000000007 (~10^9 + 7~).
Обмеження
- ~1 \le N, M, A, B, K \le 10 000~
Підзадачі та оцінювання
Щоб отримати бали за підзадачу, ваша програма повинна пройти всі тести в ній. Підзадачі:
Підзадача Бали ~N, M, A, B, K \le~
1 8 8
2 11 50
3 15 300
4 20 1000
5 16 3000
6 30 10000
Input
У першому рядку містяться числа ~N, M, A, B~ і ~K~.
Output
У першому рядку виведіть число - кількість способів, якими дівчина досягне своєї мети.
Sample Input 1
3 1 2 3 2
Sample Output 1
4
Sample Input 2
100 100 30 30 10
Sample Output 2
957270726
Notes
Усі серії стрибків для досягнення мети в першому тесті:
(0,0) → (1,0) → (3,1)
(0,0) → (1,1) → (3,1)
(0,0) → (2,0) → (3,1)
(0,0) → (2,1) → (3,1)
Бали: 100
Степан вирішив зробити Роману подарунок і купив коробку цукерок. Цукерки в коробці були розташовані в ~N~ рядах по ~M~ цукерок у кожному ряду, тобто коробка являє собою прямокутник з ~N \times M~ клітинок, у кожну з яких поміщено одну цукерку. Степан також любить цукерки, тому він не втримався і з'їв їх кілька, в результаті чого в коробці залишилося ~K~ цукерок.
Стало зрозуміло, що повноцінний подарунок він зробити не зможе, тому Степан вирішив зробити красиву композицію з цукерок, що залишилися в коробці. Він вважає красивим розташування цукерок симетрично щодо кожної з двох ліній, що проходять через середини протилежних сторін коробки. Оскільки сама коробка симетрична відносно цих ліній, спостерігати за таким розташуванням буде дуже красиво.
Напишіть програму, яка знаходить, скількома способами K цукерок можна красиво розташувати в коробці.
Input
Перший рядок містить три цілі числа – ~N, M, K~ (~1 \le N, M \le 15~, ~0 \le K < N \times M~).
Output
У першому рядку виведіть одне ціле число – кількість різних способів красиво розташувати ~K~ цукерок.
Sample Input 1
3 3 2
Sample Output 1
2
Sample Input 2
1 5 4
Sample Output 2
1
Notes
До першого прикладу:
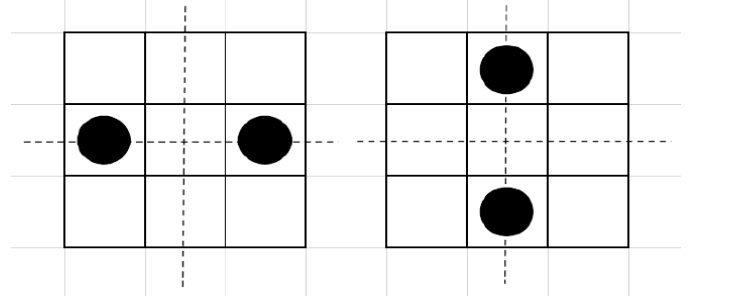
Бали: 100
Потоколяндія - це величезна країна з ~𝑁~ містами, з'єднаними ~M~ ділянками доріг, причому жодна пара міст не з'єднується більш ніж одним відрізком доріг, і кожен відрізок дороги з'єднує різні міста. Для зручності міста пронумеровані від 1 до ~𝑁~. Ділянки доріг забезпечують повне сполучення в Потоколяндії - між кожними двома містами є дорога, яка використовує ділянки дороги.
Громадяни цієї чудової країни знову перед глибоким роздумом, адже попереду чергові вибори, навіть подвійні. З огляду на майбутні вибори влада вирішила відремонтувати деякі ділянки доріг, щоб покращити сполучення між ~𝐾~ головними містами. Точніше, мета полягає в тому, щоб мати можливість подорожувати між будь-якими двома головними містами лише відремонтованими дорогами, оскільки мережа доріг Олімпії знаходиться в занедбаному стані. Ціна ремонту відома для кожної ділянки дороги.
Напишіть програму, яка, враховуючи ділянки доріг, ціни на їх ремонт і головні міста, знаходить найменшу вартість ділянок доріг, які після ремонту з'єднають головні ~𝐾~ міст, щоб ми могли дістатися від кожного головного міста до будь-якого іншого головного міста на відремонтованих ділянках доріг.
Вхідні дані
У першому рядку записані натуральні числа ~𝑁,𝐾~ і ~𝑀~ (~2 ≤ 𝐾 ≤ 𝑁 ≤ 10^5~, ~𝐾 ≤ 5~, ~1 ≤ 𝑀 ≤ 2 \times 10^5~) - кількість міст, кількість великих міст і кількість ділянок доріг.
Другий рядок містить ~𝐾~ різних натуральних числа - номери головних міст.
Наступні ~𝑀~ рядків містять по 3 цілих числа ~𝑥, 𝑦, 𝑐~, які описують ділянку дороги з двостороннім рухом між містами з номерами ~𝑥~ і ~𝑦~ з вартістю ремонту, що дорівнює ~𝑐~ (~1 ≤ 𝑐 ≤ 10^9~).
Вихідні дані
Виведіть єдине число - мінімальну загальну вартість ремонту ділянок доріг, щоб великі міста з'єднували лише відремонтовані ділянки доріг.
Оцінювання
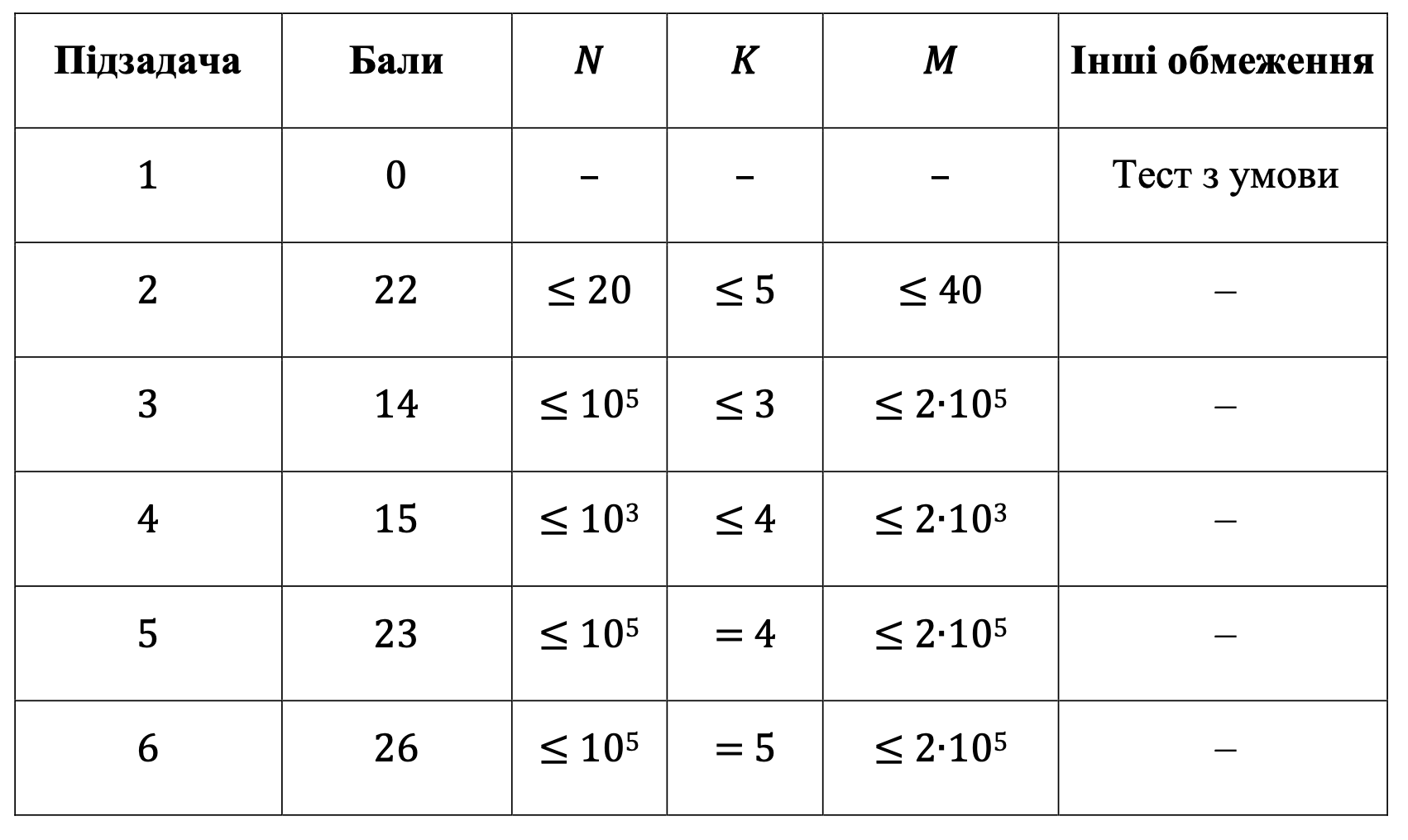
Вхідні дані #1
5 3 8
5 2 3
1 2 2
2 3 3
3 4 2
4 5 5
5 1 3
3 1 3
3 5 6
4 2 2
Вихідні дані #1
8
Пояснення до прикладу:
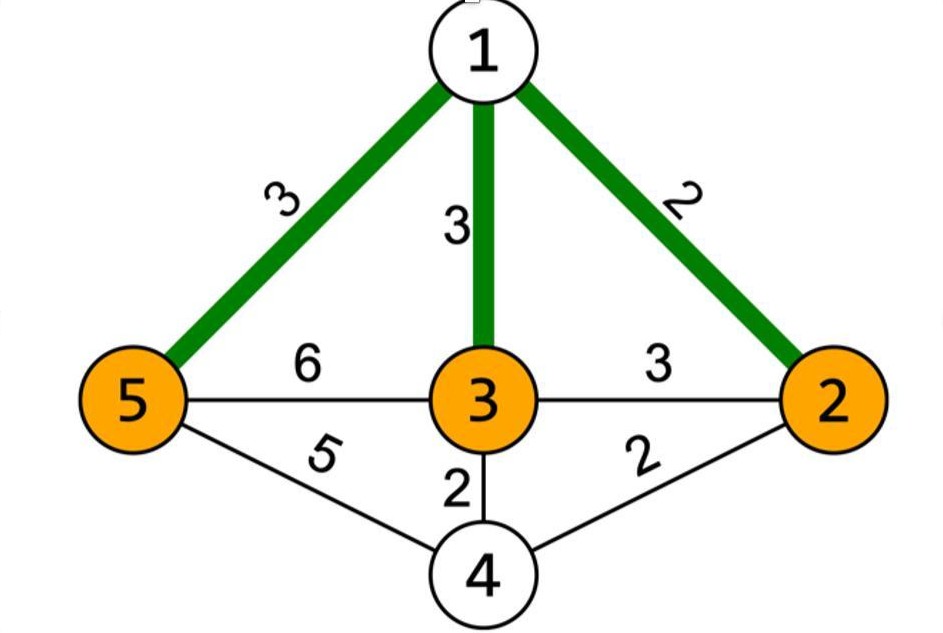
Великі міста виділені помаранчевим кольором, а оптимальні ділянки доріг для ремонту виділені жирним шрифтом і зеленим кольором. Загальна вартість їх ремонту становить 3 + 3 + 2 = 8. Вони забезпечують сполучення основних міст - у нас є дорога 5 - 1 - 3 між містами 5 і 3, дорога 5 - 1 - 2 між містами 5 і 2 і дорога 3 - 1 - 2 між містами 3 і 2.