I етап UOI 2026, 6-7 класи
Бали: 100
В Аліси зараз ~a~ гривень. Вона пам'ятає, що Боб винен їй ~b~ гривень, а Світлана винна їй ще ~c~ гривень. Проте Аліса винна Дмитру ~d~ гривень.
Якщо всі віддадуть борги, то скільки гривень буде в Аліси?
Input
Перший рядок містить одне ціле число ~a~ (~1 \leq a \leq 100~) — кількість гривень, які є в Аліси.
Другий рядок містить одне ціле число ~b~ (~1 \leq b \leq 100~) — кількість гривень, які винен Боб Алісі.
Третій рядок містить одне ціле число ~c~ (~1 \leq c \leq 100~) — кількість гривень, які винна Світлана Алісі.
Четвертий рядок містить одне ціле число ~d~ (~1 \leq d \leq 100~) — кількість гривень, які винна Аліса Дмитру.
Гарантується, що в Аліси в кінці буде невід'ємна кількість гривень.
Output
Виведіть одне ціле число — відповідь на задачу.
Sample Input 1
5
2
3
4
Sample Output 1
6
Sample Input 2
7
4
4
15
Sample Output 2
0
Бали: 100
Дано прямокутник, який складається з ~n \times m~ клітин (~n~ клітин у висоту та ~m~ клітин у ширину). Визначте площу усіх клітин, що знаходяться на межі.
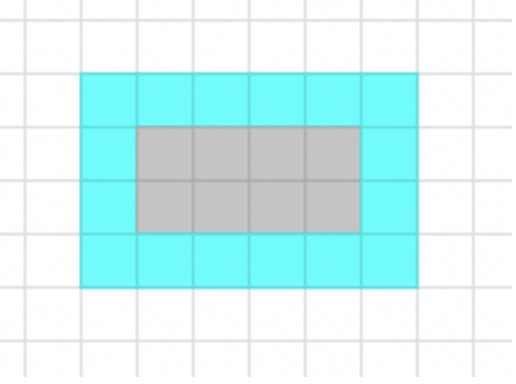
На малюнку зображено прямокутник з висотою ~n=4~ та шириною ~m=6~. Клітини, що знаходяться на межі, розфарбовані в голубий. Площа таких клітин — ~16~.
Input
Перший рядок містить одне ціле число ~n~ (~2 \leq n \leq 100~) — висота прямокутника.
Другий рядок містить одне ціле число ~m~ (~2 \leq m \leq 100~) — ширина прямокутника.
Output
Виведіть одне ціле число — відповідь на задачу.
Sample Input 1
4
6
Sample Output 1
16
Бали: 100
Після прогулянки на Гелловін Аліса і Боб назбирали мішок з ~n~ цукерками. Тепер вони хочуть розділити здобич, зігравши в наступну гру:
Аліса і Боб ходять по черзі, причому Аліса ходить першою.
Гра триває, допоки у мішку є принаймні ~3~ цукерки.
За свій хід гравець забирає собі рівно ~3~ цукерки з мішка.
Вам потрібно визначити, скільки усього цукерок забере собі Боб.
Input
Єдиний рядок вхідних даних містить одне ціле число ~n~ (~1 \leq n \leq 100~) — кількість цукерок, які Аліса і Боб зібрали на Гелловіні.
Output
Виведіть одне ціле число — відповідь на задачу.
Sample Input 1
8
Sample Output 1
3
Sample Input 2
12
Sample Output 2
6
Sample Input 3
2
Sample Output 3
0
Notes
У першому прикладі на початку гри в мішку знаходиться ~8~ цукерок.
На першому ході Аліса забирає собі ~3~ цукерки з мішка. В мішку залишається ~5~ цукерок.
На другому ході Боб забирає собі ~3~ цукерки з мішка. В мішку залишається ~2~ цукерки.
Гра закінчується, оскільки в мішку залишилось менше ніж ~3~ цукерки.
Сумарно, Боб забрав собі ~3~ цукерки, тому відповідь на задачу — ~3~.
У другому прикладі на початку гри в мішку знаходиться ~12~ цукерок.
На першому ході Аліса забирає собі ~3~ цукерки з мішка. В мішку залишається ~9~ цукерок.
На другому ході Боб забирає собі ~3~ цукерки з мішка. В мішку залишається ~6~ цукерок.
На третьому ході Аліса забирає собі ~3~ цукерки з мішка. В мішку залишається ~3~ цукерки.
На четвертому ході Боб забирає собі ~3~ цукерки з мішка. В мішку не залишається жодної цукерки.
Гра закінчується, оскільки в мішку залишилось менше ніж ~3~ цукерки.
Сумарно, Боб забрав собі ~6~ цукерок, тому відповідь на задачу — ~6~.
У третьому прикладі на початку гри в мішку знаходиться ~2~ цукерки. Оскільки на початку в мішку менше трьох цукерок, Аліса не може зробити перший хід, тому гра одразу завершується. Боб не забрав жодної цукерки, тому відповідь на задачу — ~0~.
Бали: 100
Козак Вус готується до міжгалактичної олімпіади з інформатики, кожного дня розв'язуючи по 8 задач, і сьогодні — не виключення. Проте, дійшовши до цієї задачі, він вирішив, що йому ця задача не подобається. Саме тому тепер вирішити цю задачу повинні ви.
У вас є матриця, яка складається з ~n~ рядків та ~m~ стовпчиків. На початку усі клітини незафарбовані. Ви можете зафарбувати деяку кількість клітин в цій матриці.
Матриця буде гарною, якщо на кожній антидіагоналі є хоча б одна зафарбована клітина. Антидіагоналями називають діагоналі, що йдуть зліва знизу вправо вгору.
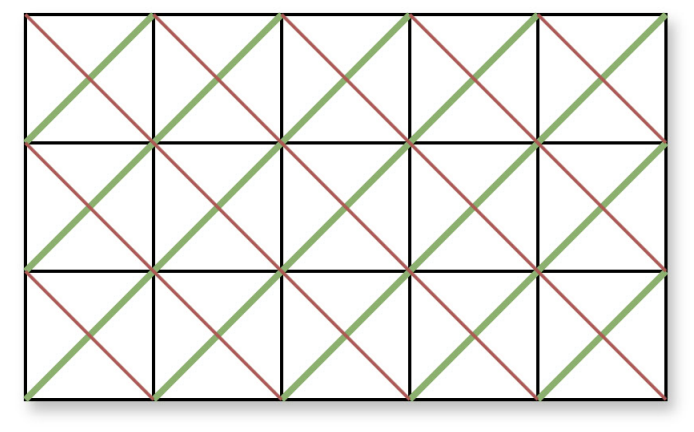
На малюнку зеленим зображені усі антидіагоналі для матриці ~n=3,m=5~, а червоним — головні діагоналі, які вас в цій задачі не цікавлять
Допоможіть Козаку Вусу і скажіть, чи можливо зафарбувати рівно ~K~ клітинок в матриці таким чином, щоб вона стала гарною.
Input
Єдиний рядок вхідних даних містить три цілі числа ~n, m, k~ (~1 \leq n, m \leq 100~; ~0 \leq k \leq n \cdot m~) — розміри матриці та кількість клітинок, яку потрібно зафарбувати відповідно.
Output
Виведіть "YES", якщо можна зафарбувати рівно ~K~ клітинок, щоб матриця стала гарною, або "NO" у іншому випадку.
Sample Input 1
3 5 7
Sample Output 1
YES
Sample Input 2
4 2 6
Sample Output 2
YES
Sample Input 3
1 1 0
Sample Output 3
NO
Sample Input 4
3 3 3
Sample Output 4
NO
Notes
У першому прикладі можна зафарбувати клітини наступним чином:
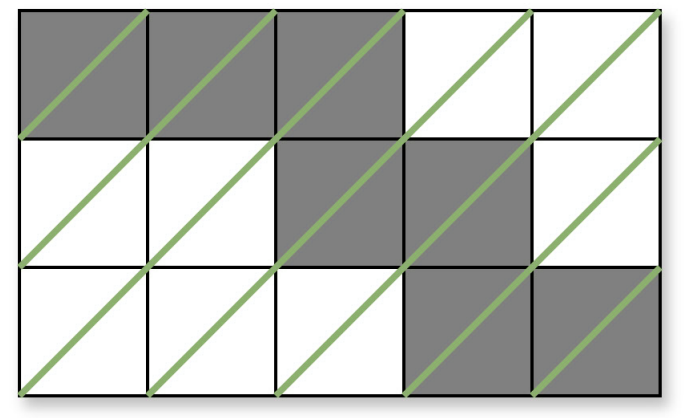
Зеленим позначено антидіагоналі, а сірим — зафарбовані клітини
У другому прикладі можна зафарбувати клітини наступним чином:
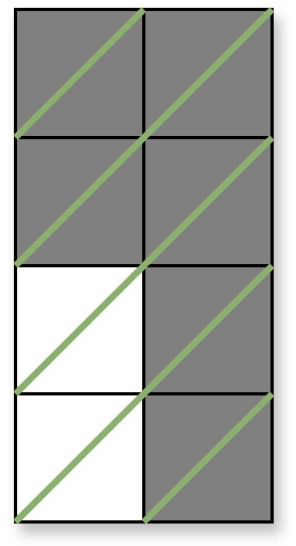
Зеленим позначено антидіагоналі, а сірим — зафарбовані клітини
У третьому та четвертому прикладах не можна зафарбувати клітини, аби матриця стала гарною.
Бали: 100
Аліса давно мріє про фірмову сумку, яка коштує ~x~ гривень. Вона має на рахунку ~n~ гривень і щойно підписала контракт на роботу терміном на ~y~ років. Щороку вона отримуватиме фіксовану зарплату ~s~ гривень.
Після завершення контракту Аліса планує купити сумку. Однак може виявитися, що зібраних грошей буде недостатньо. У такому разі вона може продовжити контракт ще на кілька (можливо, нуль) років із тією самою зарплатою.
Визначте, на яку мінімальну кількість років Алісі потрібно продовжити контракт, аби їй вистачило грошей на омріяну покупку.
Попри абсурдність ситуації, ми припускаємо, що Аліса не витрачає ці кошти ні на що інше.
Input
У єдиному рядку вхідних даних через пробіл записано чотири цілі числа ~n, x, s, y~ (~1 \leq n, x, s, y \leq 100~) — кількість наявних грошей в Аліси, ціна сумки, щорічна зарплата на контракті й довжина контракту відповідно.
Output
Виведіть одне ціле число — відповідь на задачу.
Sample Input 1
50 100 10 3
Sample Output 1
2
Sample Input 2
50 100 10 7
Sample Output 2
0
Sample Input 3
45 100 10 3
Sample Output 3
3
Notes
У першому прикладі Аліса має на рахунку ~50~ гривень, а сумка коштує ~100~ гривень. За контрактом Аліса отримує ~10~ гривень щорічно. Після ~3~ років контракту Аліса заробить ~3 \cdot 10 = 30~ гривень, тож після завершення контракту вона матиме ~50+30=80~ гривень. Якщо Аліса продовжить контракт на ще ~2~ роки, то вона матиме ~80 + 2 \cdot 10 = 100~ гривень і зможе придбати сумку.
У другому прикладі Аліса має на рахунку ~50~ гривень, а сумка коштує ~100~ гривень. За контрактом Аліса отримує ~10~ гривень щорічно. Після ~7~ років контракту Аліса заробить ~7 \cdot 10 = 70~ гривень, тож після завершення контракту вона матиме ~50+70=120~ гривень. Оскільки вона вже має достатньо грошей для придбання сумки, додатково продовжувати контракт їй не треба, тож відповідь на задачу — ~0~ років.
У третьому прикладі Аліса має на рахунку ~45~ гривень, а сумка коштує ~100~ гривень. За контрактом Аліса отримує ~10~ гривень щорічно. Після ~3~ років контракту Аліса заробить ~3 \cdot 10 = 30~ гривень, тож після завершення контракту вона матиме ~45+30=75~ гривень. Якщо Аліса продовжить контракт на ще ~3~ роки, то вона матиме ~75 + 3 \cdot 10 = 105~ гривень і зможе придбати сумку.
Бали: 100
На честь вступу в університет Козаку Вусу подарували конструктор Elgo, який складається з чотирьох кубиків. На кожному кубику написана одна цифра, зокрема, на першому кубику написана цифра ~a~, на другому — ~b~, на третьому — ~c~, а на четвертому — ~d~.
Перед сном, у ліжку, Козак Вус задумався про двозначні числа, і тепер його цікавить, чи можна з його набору кубиків зібрати два двозначні числа, використовуючи кожен кубик рівно один раз. Козак Вус економить сили перед завтрашньою лекцією, тому він просить вас відповісти на його питання.
Число, складене з декількох кубиків, вважається двозначним, якщо в ньому немає ведучих нулів і воно більше за ~9~ і менше за ~100~. Наприклад, числа ~67~ або ~33~ вважаються двозначними, а ~0020~, ~4~ та ~05~ — ні.
Input
У єдиному рядку вхідних даних через пробіл записано чотири цифри ~a, b, c, d~ (~0 \leq a, b, c, d \leq 9~) — цифри, записані на першому, другому, третьому та четвертому кубиках відповідно.
Output
Виведіть "YES", якщо Козак Вус може скласти два двозначні числа, або "NO" в іншому випадку.
Sample Input 1
1 2 3 4
Sample Output 1
YES
Sample Input 2
1 0 2 0
Sample Output 2
YES
Sample Input 3
9 0 0 0
Sample Output 3
NO
Notes
У першому прикладі Козак Вус може скласти два числа — ~32~ та ~14~.
У другому прикладі Козак Вус може скласти два числа — ~10~ та ~20~.
У третьому прикладі Козак Вус може скласти лише одне двозначне число — ~90~.
Бали: 100
Козак Вус має таємницю, яку можна представити у вигляді матриці ~T~, яка складається з ~2~ рядків, пронумерованих зверху вниз, та ~2~ стовпчиків, пронумерованих зліва направо. У цій матриці кожна комірка містить ціле невід'ємне число. Оскільки ця таємниця дуже секретна, Козак Вус не може зберігати її безпосередньо у такому вигляді, тому, аби не забути таємницю, він зберігає її наступним чином:
На аркуші Козак Вус записав ~4~ цілі невід'ємні числа ~r_1, r_2, c_1, c_2~ в такому порядку.
Сума чисел у першому рядку таємниці дорівнює ~r_1~, а у другому рядку — ~r_2~. Більш формально, ~T_{1,1} + T_{1,2} = r_1~, а ~T_{2,1} + T_{2,2} = r_2~.
Сума чисел у першому стовпчику таємниці дорівнює ~c_2~, а у другому стовпчику — ~c_2~. Більш формально, ~T_{1,1} + T_{2,1} = c_1~, а ~T_{1,2} + T_{2,2} = c_2~.
Додатково Козак Вус зберігає декілька фальшивих аркушів, на яких також записані 4 випадкові цілі числа. Ці аркуші не відповідають жодній матриці ~2~ на ~2~, яка могла бути таємницею Козака Вуса.
Нещодавно вам у руки потрапив один з тих самих аркушів, і вам стало цікаво дізнатись, чи цей аркуш фальшивий, чи цей аркуш може описувати таємницю Козака Вуса.
Всі числа мають бути у проміжку ~0 \leq T_{i,j} \leq 10^9~. Якщо таємниць ~T~, які відповідають заданому аркушу, декілька, дозволяється вивести будь-яку з них.
Input
Перший рядок вхідних даних містить два цілі числа ~r_1~ та ~r_2~ (~0 \leq r_1, r_2 \leq 10^9~) — перше та друге числа відповідно, записані на аркуші.
Другий рядок вхідних даних містить два цілі числа ~c_1~ та ~c_2~ (~0 \leq c_1, c_2 \leq 10^9~) — третє та четверте числа відповідно, записані на аркуші.
Output
У першому рядку вихідних даних виведіть "Yes", якщо аркуш може відповідати таємниці Козака Вуса, або "No", якщо цей аркуш фальшивий.
Якщо аркуш може відповідати таємниці Козака Вуса, виведіть таємницю ~T~ у наступному форматі:
У другому рядку вихідних даних виведіть через пробіл два невід'ємні цілі числа ~T_{1, 1}, T_{1, 2}~ — елементи першого рядка таємниці.
У третьому рядку вихідних даних виведіть через пробіл два невід'ємні цілі числа ~T_{2, 1}, T_{2, 2}~ — елементи другого рядка таємниці.
Sample Input 1
2 3
4 1
Sample Output 1
Yes
1 1
3 0
Sample Input 2
5 0
5 0
Sample Output 2
Yes
5 0
0 0
Sample Input 3
1 1
1 0
Sample Output 3
No
Пояснення
У першому прикладі заданий аркуш не фальшивий — він може відповідати наступній матриці ~T~:
| 1 | 1 |
|---|---|
| 3 | 0 |
Сума першого рядка цієї матриці ~1+1=2~, що відповідає першому числу, записаному на аркуші.
Сума другого рядка цієї матриці ~3+0=3~, що відповідає другому числу, записаному на аркуші.
Сума першого стовпчика цієї матриці ~1+3=4~, що відповідає третьому числу, записаному на аркуші.
Сума другого стовпчика цієї матриці ~1+0=1~, що відповідає четвертому числу, записаному на аркуші.
У другому прикладі заданий аркуш не фальшивий — він може відповідати наступній матриці ~T~:
| 5 | 0 |
|---|---|
| 0 | 0 |
Сума першого рядка цієї матриці ~5+0=5~, що відповідає першому числу, записаному на аркуші.
Сума другого рядка цієї матриці ~0+0=0~, що відповідає другому числу, записаному на аркуші.
Сума першого стовпчика цієї матриці ~5+0=5~, що відповідає третьому числу, записаному на аркуші.
Сума другого стовпчика цієї матриці ~0+0=0~, що відповідає четвертому числу, записаному на аркуші.
У третьому прикладі заданий аркуш фальшивий — він не відповідає жодній можливій матриці ~T~.
Бали: 100
Невідомим чином Козак Вус опинився на нескінченній числовій прямій у координаті ~x~. Протягом ~n~ секунд, кожної секунди ~i~ (~1 \leq i \leq n~) відбувалося наступне:
на початку ~i~-ої секунди він бачив деяке число ~y_i~.
наприкінці ~i~-ої секунди він опинявся у найближчій координаті, яка є кратною ~y_i~ (тобто, координаті, що націло ділиться на ~y_i~). Якщо таких координат декілька, він опинявся у найменшій з них.
Зверніть увагу, що він ніколи не може опинитися у від'ємній координаті.
Прокинувшись, Козак Вус зрозумів, що це був сон: він чітко пам'ятає всі ~y_i~ та тривалість сну ~n~, але не може згадати, у якій координаті опинявся наприкінці кожної секунди. Заспокойте Козака Вуса й допоможіть відновити цей дивний сон!
Input
Перший рядок містить два цілі числа ~n~ та ~x~ (~1 \leq n \leq 2 \cdot 10^5~; ~0 \leq x \leq 10^4~) — тривалість дивного сну і початкова координата Козака Вуса відповідно.
Другий рядок містить ~n~ цілих чисел ~y_1, y_2, \dots, y_n~ (~1 \leq y_i \leq 10^4~), де ~y_i~ — число, яке Козак Вус бачив на початку ~i~-ої секунди сну.
Output
Виведіть ~n~ цілих чисел ~c_1, c_2, \dots, c_n~, де ~c_i~ — координата, у якій опинявся Козак Вус наприкінці ~i~-ої секунди сну.
Sample Input 1
3 2
2 4 1
Sample Output 1
2 0 0
Sample Input 2
3 5
2 3 2
Sample Output 2
4 3 2
Sample Input 3
1 10000
5001
Sample Output 3
10002
Notes
У першому прикладі Козак Вус починає з координати ~2~.
На початку першої секунди Козак Вус бачить число ~y_1=2~. Найближчою координатою до ~2~ кратною ~2~ є ~2~. Тому наприкінці першої секунди Козак Вус залишиться у координаті ~2~.
На початку другої секунди Козак Вус бачить число ~y_2=4~. Найближчими координатами до ~2~ кратними ~4~ є ~0~ та ~4~. Оскільки ~0<4~, то наприкінці другої секунди Козак Вус опиниться у координаті ~0~.
На початку третьої секунди Козак Вус бачить число ~y_3=1~. Найближчою координатою до ~0~ кратною ~1~ є ~0~. Тому наприкінці третьої секунди Козак Вус залишиться у координаті ~0~.
У другому прикладі Козак Вус починає з координати ~5~.
На початку першої секунди Козак Вус бачить число ~y_1=2~. Найближчими координатами до ~5~ кратними ~2~ є ~4~ та ~6~. Оскільки ~4<6~, то наприкінці першої секунди Козак Вус опиниться у координаті ~4~.
На початку другої секунди Козак Вус бачить число ~y_2=3~. Найближчою координатою до ~4~ кратною ~3~ є ~3~. Тому наприкінці другої секунди Козак Вус залишиться у координаті ~3~.
На початку третьої секунди Козак Вус бачить число ~y_3=2~. Найближчими координатами до ~3~ кратними ~2~ є ~2~ та ~4~. Оскільки ~2<4~, то наприкінці третьої секунди Козак Вус опиниться у координаті ~2~.
У третьому прикладі Козак Вус починає з координати ~10^4~.
- На початку першої секунди Козак Вус бачить число ~y_1=5001~. Найближчою координатою до ~10000~ кратною ~5001~ є ~10002~. Тому наприкінці першої секунди Козак Вус опиниться у координаті ~10002~.
Ви отримаєте не менше ~10~ балів, якщо ваш розв'язок буде коректно працювати для ~n=1~.
Ви отримаєте не менше ~20~ балів, якщо ваш розв'язок буде коректно працювати для ~n \leq 2~.
Ви отримаєте не менше ~60~ балів, якщо ваш розв'язок буде коректно працювати для ~n \leq 100~ та ~max(y_1,y_2, \ldots, y_n) \leq 100~.