Леді принесла до класу дві коробки – в одній були лише рукавички для лівшів, а в іншій – лише рукавички для правшів. Рукавички могли бути як білими, так і чорними. Кожен учень, не дивлячись, взяв по одній рукавичці з кожної коробки та надів їх на руки.

Коли всі учні одягли рукавички, виявилося, що у ~A~ дітей були білі рукавички на обох руках, у ~B~ дітей була біла рукавичка на правій руці та чорна рукавичка на лівій. У ~C~ дітей були навпаки: чорна рукавичка на правій руці та біла рукавичка на лівій. Нарешті, у ~D~ дітей були чорні рукавички на обох руках.

Леді попросила учнів взятися за руки та утворити якомога довший ланцюжок, дотримуючись таких умов:

• Кожен учень повинен стояти обличчям до Леді;
• Учні можуть триматися за руки лише в тому випадку, якщо колір рукавичок на їхніх руках збігається.

Напишіть програму, яка знаходить довжину найдовшого можливого ланцюжка, який можуть учні утворити.

Формат вхідних даних:

Перший рядок містить чотири цілі числа ~A, B, C~ та ~D~ (~0 ≤ A, B, C, D ≤ 10^8~).

Формат вихідних даних:

Виведіть одне ціле число – довжину найдовшого ланцюжка, в який учні можуть розташуватися, дотримуючись умов, заданих Леді.

Система оцінювання:

Бали за кожен тест нараховуються окремо.

Приклад вхідних даних:

1 1 1 1

Приклад вихідних даних:

4

Приклад вхідних даних:

0 3 1 0

Приклад вихідних даних:

3

Пояснення до прикладів:

У Леді є число ~K~. Номер шифру до сейфа – це мінімальне число, добуток цифр якого дорівнює ~K~.

Напишіть програму, яка допоможе Леді правильно визначити номер шифру до сейфа.

Формат вхідних даних:

Перший рядок містить ціле число ~K~ (~1 ≤ K ≤ 10^{18}~).

Формат вихідних даних:

Виведіть одне ціле число, що дорівнює мінімальному значенню шифру сейфа. Якщо відповідного числа не існує, то виведіть –1.

Система оцінювання:

Бали за кожен тест нараховуються окремо.

Приклад вхідних даних:

10

Приклад вихідних даних:

25

Приклад вхідних даних:

13

Приклад вихідних даних:

-1

Дано послідовність з ~n~ цілих чисел. Виконуємо таку операцію: видаляємо перший або останній елемент послідовності. Це призводить до нової послідовності з одним елементом меншим за попередню. Ми виконуємо ту саму операцію над новою послідовністю знову та повторюємо цю операцію багаторазово, доки послідовність не матиме елементів.

Напишіть програму, яка знаходить найменшу кількість операцій описаного типу, які ми можемо застосувати, щоб сума видалених елементів стала рівною заданому числу ~k~.

Формат вхідних даних:

Перший рядок містить два цілих чисел ~n~ та ~k~ (~0 < n ≤ 10^6~, ~0 < k ≤ 10^5~).

Другий рядок містить елементи заданої послідовності, розділені пробілами. Числа в заданій послідовності є цілими, невід'ємними та меншими за 300.

Формат вихідних даних:

У єдиному рядку виведіть одне ціле число – необхідна мінімальна кількості операцій. Коли неможливо отримати суму видалених чисел, що дорівнює ~k~, виведіть число -1.

Система оцінювання:

Бали за кожен тест нараховуються окремо.

Приклади вхідних даних:

5 3
1 1 1 2 2

Приклади вихідних даних:

2

Приклади вхідних даних:

3 5
1 6 2

Приклади вихідних даних:

-1

У розпал заходів зі збору сміття, улюблена вулиця Леді була заповнена величезною кількістю листя від типового осіннього листопада.

Оскільки Леді дуже любить чистоту, вона поставила собі завдання прибрати тротуар на вулиці.

Точніше, тротуар має ~N~-метрову довжину, розділений на ~N~ однометрові секції, пронумеровані відповідно до їхнього положення зліва направо вздовж вулиці, де на ~i~–й секції зібрано ~V_i~ кубічних метрів листя. Кожен кубічний метр листя важить 1 кілограм. За 1 метр ліворуч від першої секції тротуару знаходиться колекція з ~K~ сміттєвих пакетів, відповідно, кожен з них міг би вмістити всю кількість листя на тротуарі. Кожен пакет має свою вагу ~C~. Для спрощення позначимо джерело пакетів як позицію 0.

Спочатку Леді знаходиться поруч із джерелом пакетів. Щоб очистити тротуар, вона може виконати кілька дій. Нехай вона знаходиться в секції ~X~ і несе ~W~ кілограмів (загальна вага пакета та листя). Тоді вона може:

• зібрати 1 кілограм листя з поточної секції, в якій вона знаходиться (~V_X → V_X - 1~), та покласти їх у свій пакет. Вона повинна мати ~X > 0~ та ~V_X > 0~, що коштуватиме їй 0 одиниць зусиль.
• переміститися на одну секцію ліворуч (~X → X - 1~), якщо ~X > 0~. Це коштуватиме їй ~W~ одиниць зусиль.
• переміститися на одну клітинку праворуч (~X → X + 1~). Вона повинна мати ~X < N~ та ~V_X = 0~, інакше їй буде важко пройти крізь листя. Це коштуватиме їй ~W~ одиниць зусиль.
• залишити поточний пакет для листя біля джерела. Вона повинна мати ~X = 0~ і залишити собі пакет для листя, що коштуватиме їй 0 одиниць зусиль.
• взяти пакет для листя біля джерела. Вона повинна мати ~X = 0~ і не залишати пакет для листя, що коштуватиме їй 0 одиниць зусиль.

Мета Леді – зібрати все листя на тротуарі в пакети, і кожен пакет має бути на початку після завершення прибирання.

Напишіть програму, яка знаходить мінімальну кількість зусиль для прибирання тротуару.

Формат вхідних даних:

Перший рядок містить три цілих числа ~N, K, C~ (~1 ≤ K ≤ N ≤ 10^6~) – довжина тротуару, кількість пакетів та вага кожного пакета.

Другий рядок вхідних даних містить ~N~ додатних цілих чисел ~V_1~ ~V_2~ … ~V_N~ (~1 ≤ V_i ≤ 10^{12} ,~ ~\sum_{i=1}^{N}V_i \le 10^{12}~- кількість листя на ділянках.

Формат вихідних даних:

Виведіть одне ціле число – мінімальні зусилля для очищення тротуару.

Система оцінювання:

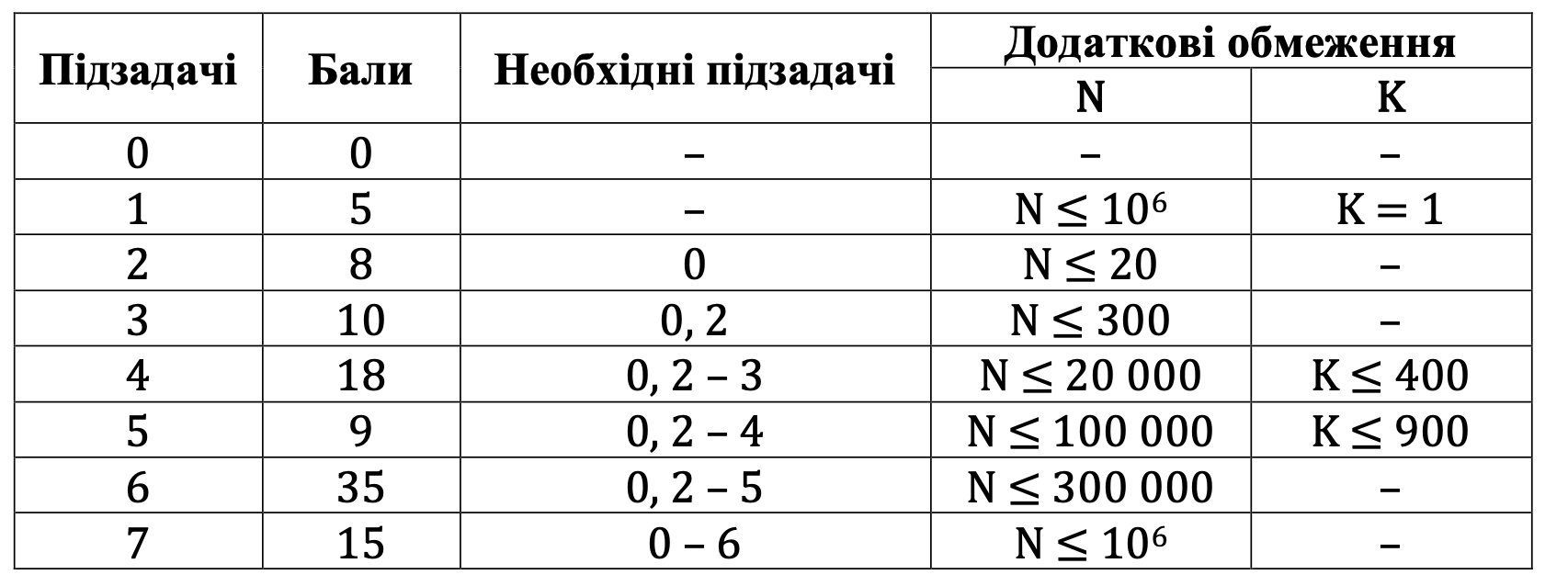
Бали за кожну підзадачу нараховуються за умови проходження усіх тестів підзадачі, залежності від підзадач немає.

Приклади вхідних даних:

7 4 1
4 3 6 8 2 10 1

Приклади вихідних даних:

199

Приклади вхідних даних:

8 2 1
2 1 1 3 1 2 1 4

Приклади вихідних даних:

133

Приклади вхідних даних:

8 2 100
2 1 1 3 1 2 1 4

Приклади вихідних даних:

1765

Леді хоче наступного дня виконати ~N~ завдань, пронумерованих від 1 до ~N~. Вона хоче визначити порядок, у якому вони будуть виконуватися, тому вона складе план. Він складатиметься з певної кількості уподобань – упорядкованих пар (~x, y~) (~1 ≤ x, y ≤ N~ та ~x ≠ y~), таких що вона віддасть перевагу виконанню завдання x перед виконанням завдання ~y~. Більш формально, план складається з певної кількості упорядкованих пар (можливо, нуль) – уподобань, причому жодні упорядковані пари не є однаковими або будь-які упорядковані пари вигляду (~x, x~).

Зауважте, що для заданого плану Леді віддасть перевагу виконанню завдання ~u~ перед завданням ~v~, якщо існує послідовність уподобань, що веде від ~u~ до ~v~. Наприклад, якщо у нас є пари уподобань (1, 2), (2, 3), (3, 4) та (2, 5), то деякі уподобання Леді включатимуть виконання завдання 1 перед 2, 3, 4 та 5, але вона не матиме уподобань щодо того, яке з завдання 4 та 5 виконувати першою.

Оскільки не всі уподобання можуть бути задоволені для заданого плану, Леді виконає якомога більше завдань, які задовольняють уподобання. Це означає, що вона зможе визначити порядок виконання цих завдань, у якому не буде порушення уподобань. Якщо для заданого плану Леді може виконати не більше ніж ~t~ завдань, то існує порядок цих завдань ~a_1, a_2, …, a_t~, такий, що немає двох завдань ~a_j~ та ~a_i~ для ~j > i~, для яких Леді віддає перевагу виконанню завдання ~a_j~ перед завданням ~a_i~.

Тепер Леді цікавиться, скільки існує можливих планів, для яких найбільша кількість завдань, яку вона може виконати, задовольняючи її вподобання, дорівнює рівно ~K~.

Допоможіть їй, написавши програму, яка знаходить кількість можливих планів для цього за модулем 12289.

Вхідні дані:

Перший рядок містить два цілих числа ~N~ та ~K~ (~1 ≤ N ≤ 650~, ~1 ≤ K ≤ N~) – кількість завдань та найбільша кількість завдань, які можна виконати відповідно до уподобань плану.

Вихідні дані:

Виведіть одне число – знайдена кількість планів за модулем 12289.

Система оцінювання:

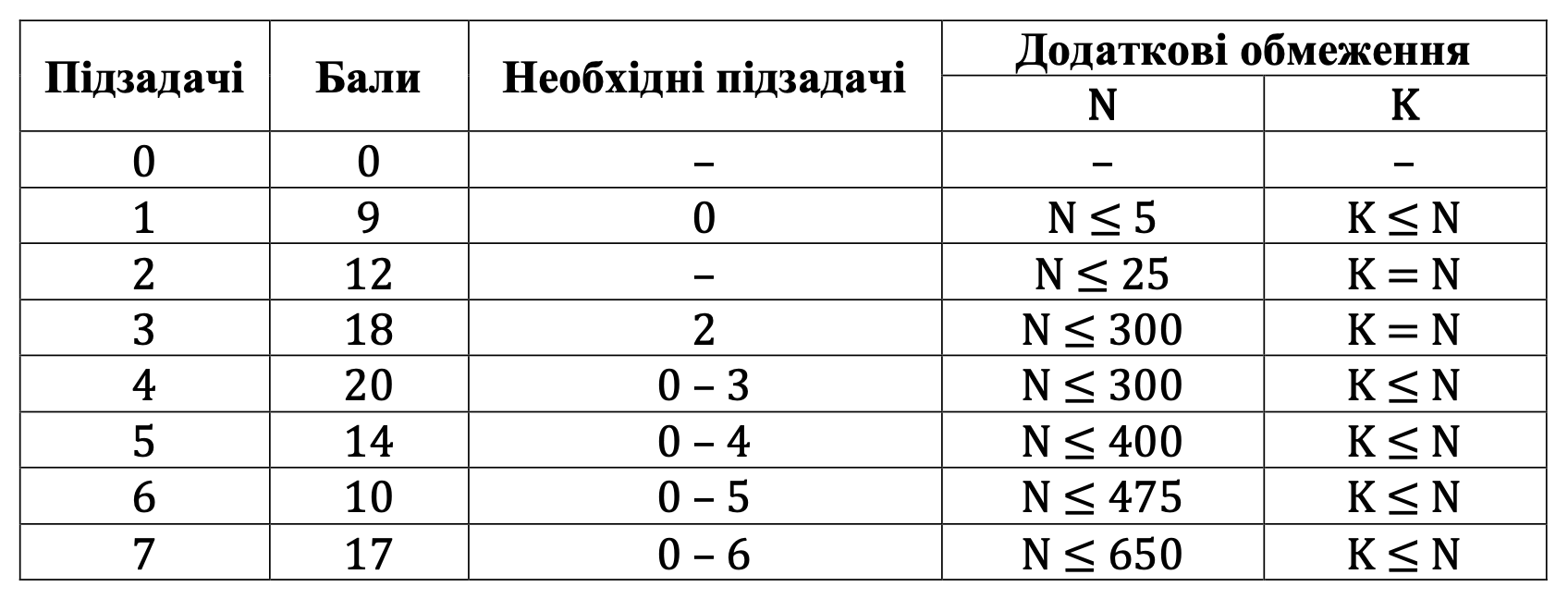
Бали за кожну підзадачу нараховуються за умови проходження усіх тестів підзадачі, залежності від підзадач немає.

Приклад вхідних даних:

2 2

Приклад вихідних даних:

3

Приклад вхідних даних:

3 1

Приклад вихідних даних:

18

Приклад вхідних даних:

4 3

Приклад вихідних даних:

774

Пояснення до першого прикладу:

Якщо представити уподобання у вигляді стрілок, то три можливі плани з максимум двома діями для виконання: