Піксельний равлик --- це така фігура, яку дуже просто намалювати на аркуші в клітинку і яка дуже схожа на лігатуру at (@).

Піксельний равлик ~k~-го порядку будується за таким алгоритмом:

• Зафарбовується <<рамка>> --- клітинки по периметру квадрата зі стороною ~k~.
• Зафарбовується клітинка, лівий верхній кут якої збігається з правим нижнім кутом рамки. Назвемо цю клітинку <<мостом>>.
• Зафарбовуються всі клітинки ззовні на відстані в одну клітинку від рамки. При цьому не зафарбовуються ті клітинки, які дотикаються до моста (за винятком клітинки, лівий нижній кут якої збігається з правим верхнім кутом моста: вона все одно зафарбовується).

На малюку нижче наведені піксельні равлики 1-го, 2-го, 3-го та 4-го порядків.

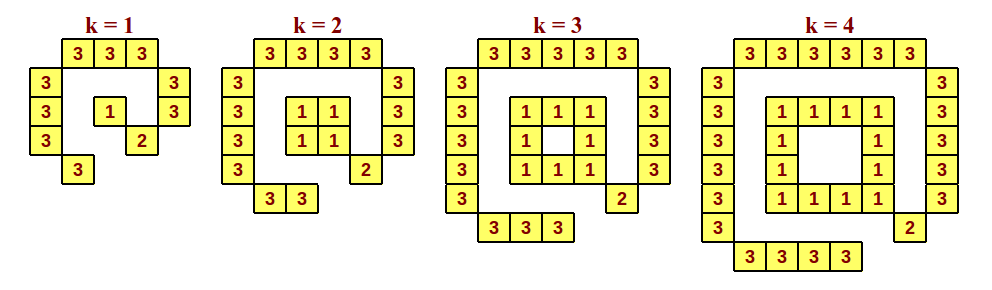
Цифрами (1, 2, 3) позначено клітинки, які зафарбовуються відповідно на першому, другому та третьому кроках алгоритму.

Напишіть програму, що знайде кількість клітинок, які потрібно зафарбувати, щоб намалювати піксельного равлика ~k~-го порядку.

Формат вхідних даних

Перший рядок містить одне ціле число ~k~ (~1 \le k \le 10^{8}~).

Формат вихідних даних

Виведіть одне число --- кількість клітинок, які потрібно зафарбувати, щоб намалювати піксельного равлика ~k~-го порядку.

Оцінювання

Якщо ваша програма буде виводити правильну відповідь для всіх ~k~ від ~1~ до ~10~, то ви отримаєте ~40~ балів.

Приклад вхідних даних

2

Приклад вихідних даних

18

Приклад вхідних даних

3

Приклад вихідних даних

26

В останні хвилини роботи відділення Нової Пошти надійшло термінове замовлення на доставлення п'яти великогабаритних вантажів. У розпорядженні відділення залишилося всього дві автівки: перша з вантажністю ~M_1~, а друга з вантажністю ~M_2~. Водія першої автівки звати Василь (Vasyl), а водія другої --- Петро (Petro).

З'ясуйте, як краще розподілити вантажі по автівках, щоб виконати замовлення.

Формат вхідних даних

Перший рядок містить п'ять цілих чисел ~m_1~, ~m_2~, ~m_3~, ~m_4~, ~m_5~ (~1 \leq m_1, m_2, m_3, m_4, m_5 \leq 100~) --- маси вантажів у тоннах.

Другий рядок містить два цілі числа ~M_1~ та ~M_2~ (~1 \leq M_1, M_2 \leq 100~) --- вантажність автівок Василя та Петра відповідно.

Формат вихідних даних

Якщо виконати замовлення неможливо, виведіть They can not do it!.

Якщо і Василь, і Петро можуть виконати замовлення самостійно, то виведіть They both can do it!.

Якщо замовлення можливо виконати за допомогою однієї автівки, але тільки одна з автівок має достатню вантажність, то виведіть, хто це має зробити: Vasyl can do it! або Petro can do it!.

Якщо виконати замовлення можливо, але для цього потрібні обидві автівки, виведіть будь-який варіант розподілення вантажів по автівках у такому форматі:

• У першому рядку виведіть They need to work together!.
• У другому рядку виведіть ім'я Vasyl, двокрапка, пробіл, номери вантажів, які треба завантажити в першу автівку.
• У третьому рядку виведіть ім'я Petro, двокрапка, пробіл, номери вантажів, які треба завантажити в другу автівку.

Номери вантажів можна виводити у будь-якому порядку.

Приклад вхідних даних

10 10 10 10 10
20 20

Приклад вихідних даних

They can not do it!

Приклад вхідних даних

5 5 5 5 5
25 30

Приклад вихідних даних

They both can do it!

Приклад вхідних даних

5 5 5 5 5
30 20

Приклад вихідних даних

Vasyl can do it!

Приклад вхідних даних

5 5 5 5 5
10 25

Приклад вихідних даних

Petro can do it!

Приклад вхідних даних

7 8 9 10 11
30 30

Приклад вихідних даних

They need to work together!
Vasyl: 1 2
Petro: 3 4 5

Приклад вхідних даних

7 8 9 10 11
30 31

Приклад вихідних даних

They need to work together!
Vasyl: 1 2
Petro: 5 3 4

Василь та Петро тренують пам'ять. Для цього вони беруть масив ~A[1..n]~ із ~n~ елементів та виконують такі дії:

• спочатку Василь забирає собі будь-яке число з цього масиву та називає в довільному порядку всі інші елементи масиву;
• потім Петро робить аналогічні дії з масивом, елементи якого назвав Василь, тобто забирає собі будь-яке число з цього масиву та називає в довільному порядку всі інші елементи масиву;
• потім свій хід знову робить Василь;
• потім знову Петро;
• і так далі.

Очевидно, що після ~n~ ходів усі елементи масиву ~A~ будуть розподілені між Василем та Петром.

Розглянемо на прикладі, як відбувається тренування пам'яті. Нехай початковий масив ~A = [1\; 2\; 3\; 4\; 5\; 6]~.

• Першу дію виконує Василь: ~[3\; 6\; 1\; 2\; 4]~. Він забрав собі число ~5~ та назвав у довільному порядку всі інші елементи масиву ~A~.
• Далі Петро називає такий масив: ~[2\; 6\; 3\; 4]~. Він забрав собі число ~1~.
• Далі Василь називає такий масив: ~[3\; 4\; 6]~. Він забрав собі число ~2~.
• Далі Петро називає такий масив: ~[4\; 3]~. Він забрав собі число ~6~.
• Далі Василь називає такий масив: ~[3]~. Він забрав собі число ~4~.
• Петро забирає собі останнє число ~3~.
• Отже, у Василя опинилися числа ~[2\;4\; 5]~, а в Петра ~[1\; 3\; 6]~.

Напишіть програму, яка за заданим масивом та перебігом подій з'ясує, хто які елементи забрав собі.

Формат вхідних даних

Перший рядок містить одне ціле число ~n~ (~2 \le n \le 1\,000~) --- кількість елементів у масиві ~A~.

Другий рядок містить ~n~ цілих чисел ~a_1, a_2, \dots, a_n~ (~-10^9 \le a_i \le 10^9~).

Кожен з наступних ~(n-1)~ рядків містить масив, який називав Василь або Петро. Гарантується, що масиви правильні, тобто кожен такий масив можна отримати з попереднього.

Формат вихідних даних

У першому рядку виведіть у порядку неспадання елементи, які забрав собі Василь.

У другому рядку виведіть у порядку неспадання елементи, які забрав собі Петро.

Оцінювання

У цій задачі кожен тест оцінюється окремо. Проте також:

• У 22\% тестів у початковому масиві ~A~ кожне ціле число від ~1~ до ~n~ трапляється рівно один раз.
• У 35\% тестів ~n \leq 10~.

Приклад вхідних даних

6
1 2 3 4 5 6
3 6 1 2 4
2 6 3 4
3 4 6
4 3
3

Приклад вихідних даних

2 4 5 
1 3 6

Приклад вхідних даних

5
1 8 4 2 100
2 4 100 8
100 2 8
2 8
2

Приклад вихідних даних

1 2 100 
4 8

Вимірювання земельної ділянки ~-~ важлива геодезична процедура. Щоб отримати точні числові показники, процедуру вимірювання повинні виконувати професійні геодезисти.

Розглянемо таку задачу. Нехай є квадратна ділянка, яку геодезисти розділили на ~n^2~ прямокутних ділянок, провівши ~(n-1)~ вертикальних ліній та ~(n-1)~ горизонтальних ліній. Пронумеруємо стовпчики та рядки діляночок так, як вказано на малюнку (масштабу не дотримано). Тобто рядки нумеруються знизу вгору цілими числами від ~1~ до ~n~; а стовпчики нумеруються зліва направо цілими числами від ~1~ до ~n~.

Ділянки, які знаходяться на перетині ~i~-го стовпчика та ~i~-го рядка ~(1 \le i \le n)~, будемо називати головною діагоналлю. Ділянки, які знаходяться на перетині ~(i+1)~-го стовпчика та ~i~-го рядка ~(1 \le i \le n-1)~, будемо називати побічною діагоналлю.

Вам відомі площі ділянок на головній та побічній діагоналях. Обчисліть площу ділянки, що знаходиться на перетині ~p~-го стовпчика та ~q~-го рядка.

Формат вхідних даних

Перший рядок містить одне ціле число ~n~ (~2 \le n \le 1\,000~).

Другий рядок містить ~n~ цілих чисел ~a_1, a_2, \dots, a_n~ (~1 \leq a_i \leq 10^9~) --- площі ділянок на головній діагоналі.

Третій рядок містить ~n-1~ цілих чисел ~b_1, b_2, \dots, b_{n-1}~ (~1 \leq b_i \leq 10^9~) --- площі ділянок на побічній діагоналі.

Четвертий рядок містить два цілі числа ~p~ та ~q~ (~1 \leq p, q \leq n~) --- координати ділянки, площу якої треба обчислити.

Формат вихідних даних

Виведіть площу ділянки, що знаходиться на перетині ~p~-го стовпчика та ~q~-го рядка.

Ми хочемо знати точне значення площі, тому відповідь треба виводити у факторизованому вигляді. Іншими словами, відповідь треба представити як декілька рядків, кожен з яких містить два цілі числа ~p_i~ та ~s_i~: число ~p_i~ обов'язково просте та всі числа ~p_i~ різні, а число ~s_i~ --- ціле та не дорівнює нулю. Шукана площа має дорівнювати: ~ S = p_1^{s_1} \cdot p_2^{s_2} \cdot p_3^{s_3} \ldots p_k^{s_k}, ~ де ~k~ --- кількість рядків у відповіді. Рядки треба відсортувати за зростанням простих чисел ~p_i~. Нагадаємо, що число ~X~ вважається простим, якщо воно має рівно два цілі додатні дільники: ~1~ та ~X~.

Якщо шукана площа дорівнює 1, то виведіть дві одиниці: 1 1

Оцінювання

• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться на головній або побічній діагоналі. (~p - 1 = q~ або ~p = q~)
• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться на перетині ~i~-го стовпчика та ~(i+1)~-го рядка. (~p + 1 = q~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~10\,000~. Ділянка, площу якої треба обчислити, знаходиться на головній або побічній діагоналі. (~p - 1 = q~ або ~p = q~)
• (~5~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться на головній або побічній діагоналі. (~p - 1 = q~ або ~p = q~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~10\,000~. Ділянка, площу якої треба обчислити, знаходиться на перетині ~i~-го стовпчика та ~(i+1)~-го рядка. (~p + 1 = q~)
• (~5~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться на перетині ~i~-го стовпчика та ~(i+1)~-го рядка. (~p + 1 = q~)
• (~5~ балів): Кількість ділянок дорівнює ~25~ (~n = 5~). Площі всіх відомих ділянок не перевищують ~100~.
• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться у лівому верхньому куті. (~p=1~, ~q=n~)
• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться у правому нижньому куті. (~p=n~, ~q=1~)
• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться над головною діагоналлю. (~p < q~)
• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться під головною діагоналлю. (~p > q~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~100~. Ділянка, площу якої треба обчислити, знаходиться у лівому верхньому куті. (~p=1~, ~q=n~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~100~. Ділянка, площу якої треба обчислити, знаходиться у правому нижньому куті. (~p=n~, ~q=1~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~100~. Ділянка, площу якої треба обчислити, знаходиться над головною діагоналлю. (~p < q~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~100~. Ділянка, площу якої треба обчислити, знаходиться під головною діагоналлю. (~p > q~)
• (~5~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться у лівому верхньому куті. (~p=1~, ~q=n~)
• (~5~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться у правому нижньому куті. (~p=n~, ~q=1~)
• (~8~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться над головною діагоналлю. (~p < q~)
• (~7~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться під головною діагоналлю. (~p > q~)

Пояснення

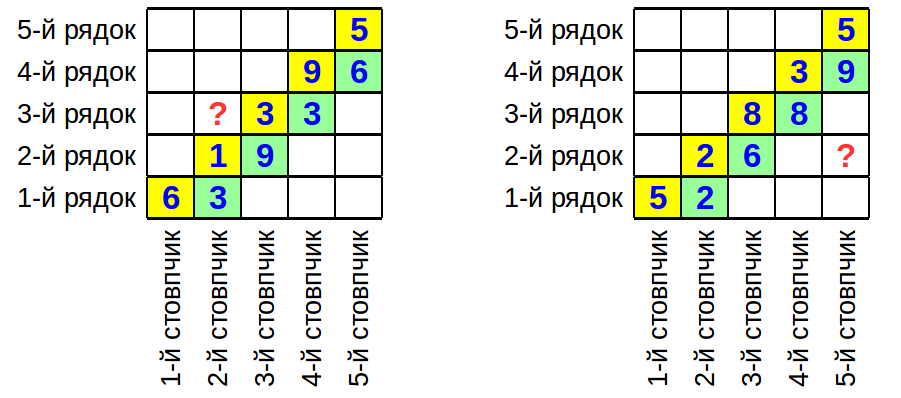
Ділянка, що знаходиться на малюнку ліворуч, відповідає першому тесту з умови. Площа ділянки на перетині 2-го стовпчика та 3-го рядка дорівнює: ~ S = 3^{-1} = \frac{1}{3} ~

Ділянка, що знаходиться на малюнку праворуч, відповідає другому тесту з умови. Площа ділянки на перетині 5-го стовпчика та 2-го рядка дорівнює: ~ S = 2^{1} \cdot 3^2 = 18 ~

Приклад вхідних даних

5
6 1 3 9 5
3 9 3 6
2 3

Приклад вихідних даних

3 -1

Приклад вхідних даних

5
5 2 8 3 5
2 6 8 9
5 2

Приклад вихідних даних

2 1
3 2

Приклад вхідних даних

5
6 1 3 9 5
3 9 3 6
2 4

Приклад вихідних даних

1 1

Еолімп пропонує вам зіграти з тестувальною системою в цікаву інтерактивну гру <<Квадрат чи прямокутник>>.

В Еолімпа є квадратна дошка розміром ~100 \times 100~ клітинок. Рядки дошки пронумеровані цілими числами від ~1~ до ~100~ зверху донизу, а стовпчики --- цілими числами від ~1~ до ~100~ зліва направо. Відповідно, клітинка, яка знаходиться у лівому верхньому куті дошки, має координати ~(1,\,1)~; клітинка, яка знаходиться у правому нижньому куті, має координати ~(100,\,100)~; а клітинка, яка знаходиться на перетині ~i~-го рядка та ~j~-го стовпчика, має координати ~(i,\,j)~.

Еолімп зафарбовує прямокутну ділянку дошки, верхній лівий кут якої має координати ~(x_1,\,y_1)~, а правий нижній --- ~(x_2,\,y_2)~. Ці координати Еолімп тримає в таємниці. Але відомо, що площа зафарбованої ділянки займає не менш ніж 4\% від площі всієї дошки.

Про будь-яку клітинку ви можете спитати в Еолімпа (чи належить вона зафарбованій ділянці) та отримати чесну відповідь від тестувальної системи. Вам треба з'ясувати, чи є зафарбована ділянка квадратом.

Прямокутник та квадрат

Протокол взаємодiї

Щоб дізнатися, чи належить клітинка зафарбованій ділянці, треба це спитати у Еолімпа. Для цього потрібно одному рядку вивести символ <> та два цілі числа ~x~ та ~y~ ~(1 \le x \le 100, \; 1 \le y \le 100)~ --- координати точки, яку ви хочете запитати. Після цього вам потрібно вивести символ нового рядка та виконати операцію flush. Після цього потрібно зчитати рядок. Еолімп виведе або <<inside>>, якщо клітинка зафарбована, або <<outside>> інакше.

• fflush(stdout) або cout.flush() в C++;

• System.out.flush() в Java;

• flush(output) в Pascal;

• stdout.flush() в Python;

• для всіх інших мов вам потрібно дивитися документацію самостійно.

Ви можете поставити не більше ~10\,000~ питань.

Коли ви будете знати відповідь, вам потрібно вивести символ <>, пробіл, та один з двох варіантів: або <<square>> (якщо зафарбована Еолімпом фігура --- квадрат), або <<rectangle>> (якщо фігура --- прямокутник).

Якщо ви не будете дотримувалися формату взаємодії, то ви можете отримати будь-який вердикт: Неправильна відповідь, Помилка виконання, Перевищено обмеження часу, тощо.

Оцінювання

Ваша програма зіграє з Еолімпом у цю гру велику кількість разів. Нехай ~q~ --- максимальна кількість питань, які ви поставили у всіх іграх. Тоді ви отримаєте таку кількість балів:

• Якщо у будь-якій грі ви поставили більше ~10\,000~ питань, вивели неправильну відповідь або не дотримувалися формату взаємодії, ви отримаєте ~0~ балів.
• Якщо ~1\,000 < q \leq 10\,000~, ви отримаєте ~5~ балів.
• Якщо ~100 < q \leq 1\,000~, ви отримаєте ~19~ балів.
• Якщо ~50 < q \leq 100~, ви отримаєте ~20 + \lfloor\frac{(100 - q) \cdot 30}{50}\rfloor~ балів.
• Якщо ~33 < q \leq 50~, ви отримаєте ~50 + \lfloor\frac{(50 - q) \cdot 50}{17}\rfloor~ балів.
• Якщо ~q \leq 33~, ви отримаєте ~100~ балів.

Пояснення

У прикладі Еолімп зафарбував ділянку, у якої верхній лівий кут --- (20, 20), а правий нижній --- (80, 80).

В умові наведений приклад того, як можна взаємодіяти з Еолімпом. Ваші запити до Еолімпа можуть бути іншими.

Приклад вхідних даних

inside
inside
outside
inside
outside
outside
inside
outside
outside

Приклад вихідних даних

? 50 50
? 75 75
? 10 10
? 20 20
? 19 20
? 20 19
? 80 80
? 81 80
? 80 81
! square