Козак Вус працює в галереї, йому доручили завдання --- побудувати якнайвищу вежу з ваз.

У нього в розпорядженні є три вази з висотами ~a~, ~b~, ~c~. Але, от лихо, якщо поставити три вази одна на одну, --- така конструкція швидко розіб'ється. Козак може вибрати лише дві вази та поставити їх одна на одну. Він хоче отримати найвищу композицію з ваз.

Знайдіть максимальну висоту, яку він може досягти.

Формат вхідних даних

Перший рядок містить три цілі числа ~a~, ~b~, ~c~ (~1 \le a,b,c \le 10^8~).

Формат вихідних даних

Виведіть одне ціле число --- максимальну висоту композиції, що задовольняє умову.

Пояснення

У першому прикладі можемо взяти першу та другу вази. Висота композиції буде ~7+4=11~.

У другому прикладі можемо взяти другу та третю вази. Висота композиції буде ~2+6=8~. Також можна взяти першу вазу замість другої.

Приклад вхідних даних

7 4 3

Приклад вихідних даних

11

Приклад вхідних даних

2 2 6

Приклад вихідних даних

8

Песика атакували злі бджоли. Для того, щоб від них сховатись, добрі смурфики побудували ~n~ куполів.

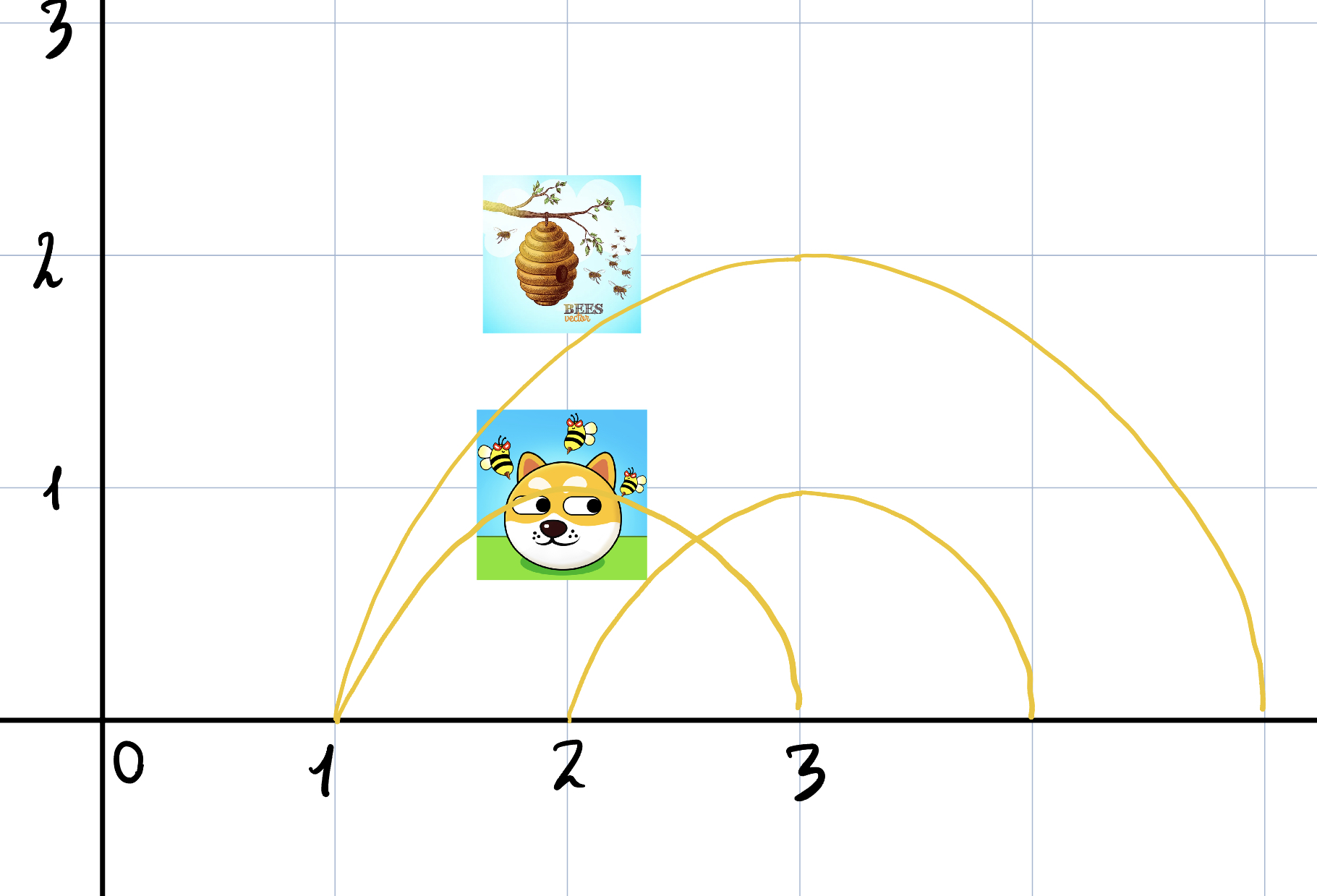
Математично купол --- це півколо, яке має центр у точці ~(pos_i,0)~ і має радіус ~r_i~, через стінку купола неможливо пройти. Песика і вулик можна представити як дві точки ~(x_1,y_1)~ та ~(x_2,y_2)~, якщо точка лежить на куполі, то вважатимемо, що точка всередині нього.

Допоможіть песику дізнатись, чи в безпеці він. Тобто чи зможуть бджоли дістатися песика, не перетинаючи куполи.

Формат вхідних даних

Перший рядок містить п'ять цілих чисел ~n~, ~x_1~, ~y_1~, ~x_2~, ~y_2~ ~(1 \le n \le 10^3, 0 \le x_1,y_1,x_2,y_2 \le 10^3)~.

Кожен з наступних ~n~ рядків містить по два цілі числа ~pos_i~ та ~r_i~ ~(0 \le pos_i \leq 10^3~; ~1 \leq r_i \le 10^3)~.

Формат вихідних даних

Якщо бджоли можуть дістатися песика, не перетинаючи стінки куполів, виведіть ~YES~.

Інакше, у першому рядку виведіть ~NO~, а в другому виведіть найменший індекс (починаючи з одиниці) купола, який розділяє бджіл та песика.

Примітка

Пояснення до першого тесту:

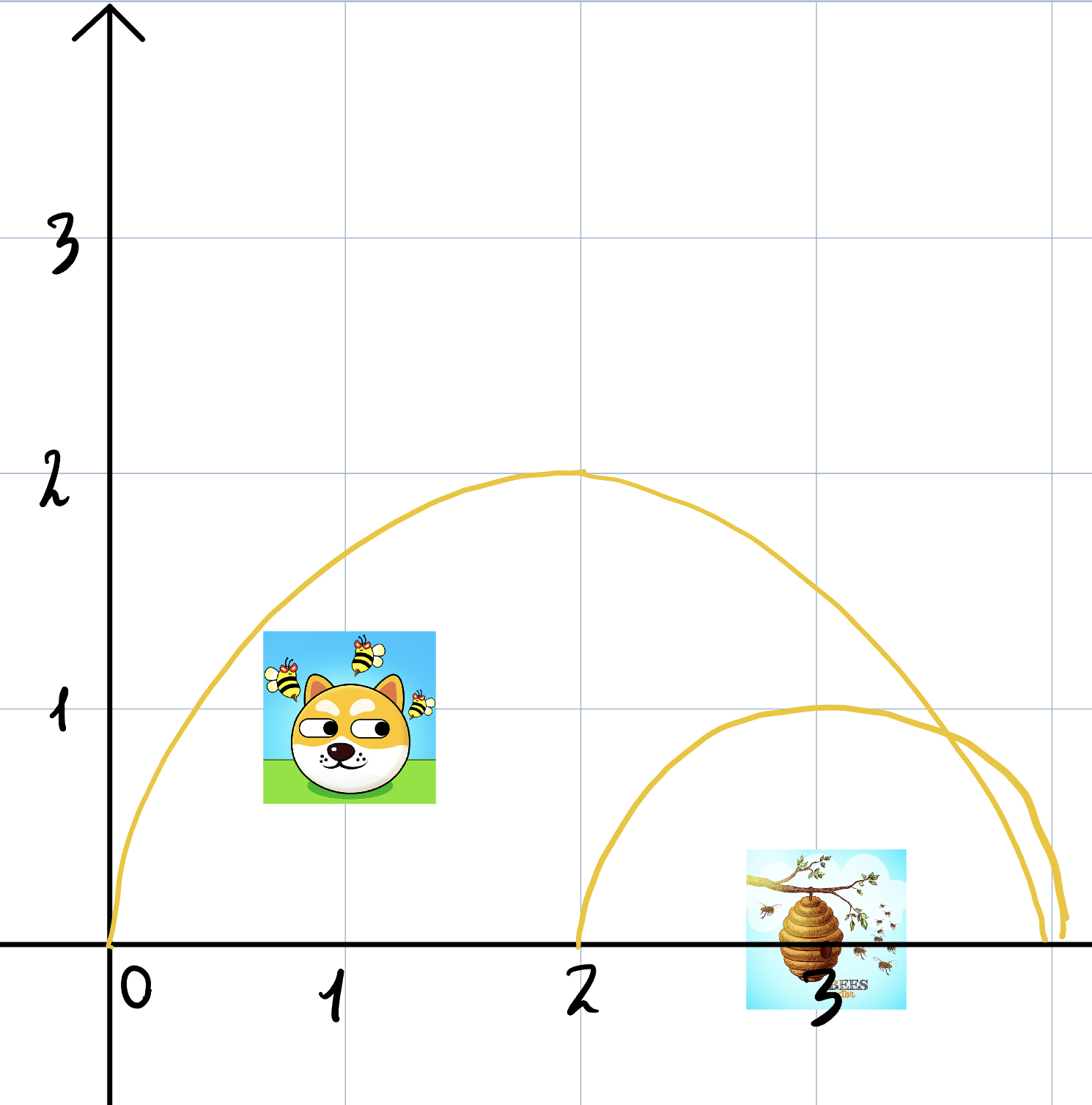
Пояснення до другого тесту:

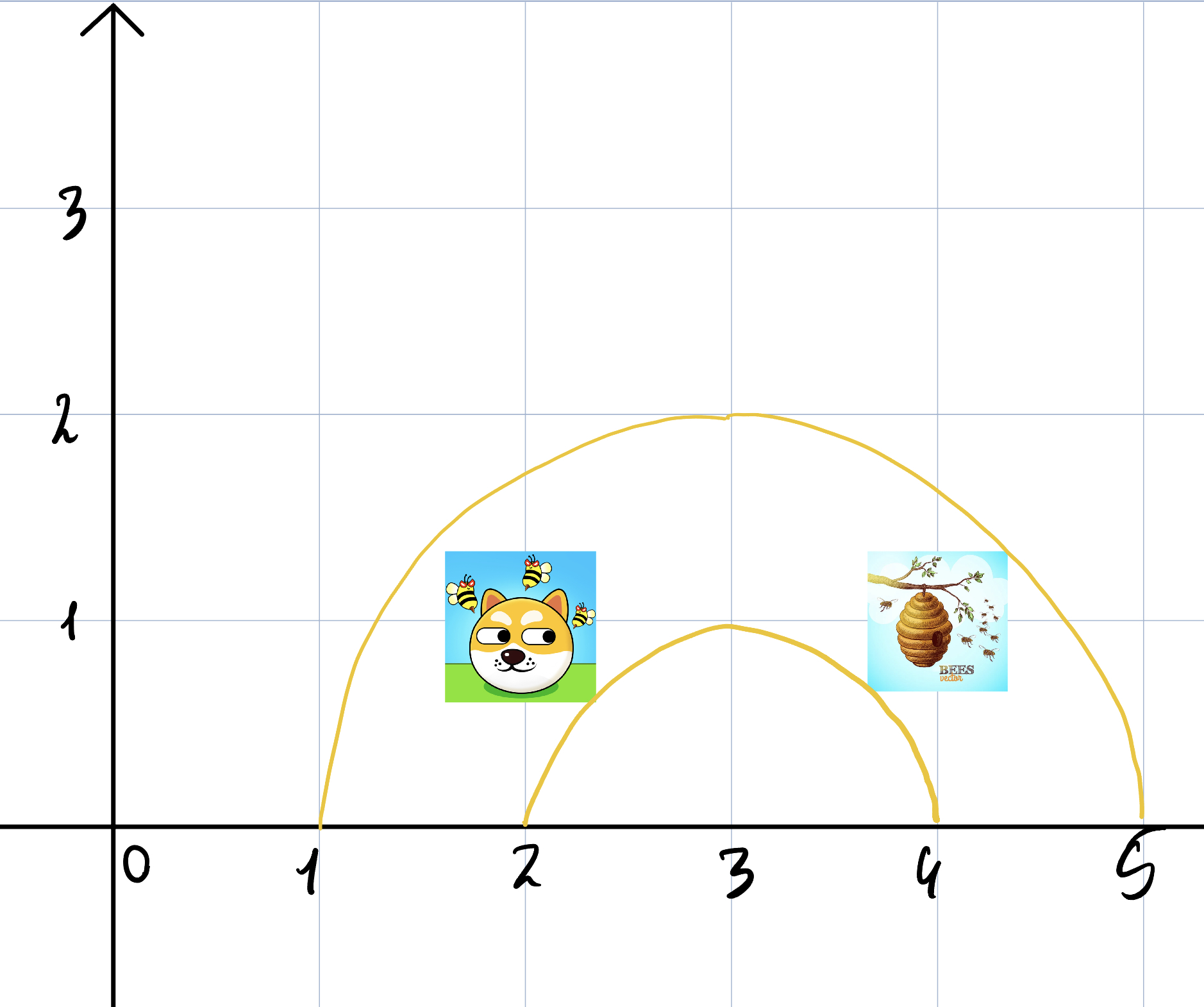
Пояснення до третього тесту:

Приклад вхідних даних

3 2 1 2 2
2 1
3 2
3 1

Приклад вихідних даних

NO
1

Приклад вхідних даних

2 1 1 3 0
2 2
3 1

Приклад вихідних даних

NO
2

Приклад вхідних даних

2 2 1 4 1
3 2
3 1

Приклад вихідних даних

YES

У Потоколяндії ~n~ міст та ~n~ двосторонніх доріг. ~i~-а дорога з'єднує міста ~i~ та ~(i+i)~ (якщо ~i+i>n~, то ~i+i-n~).

Наприклад, якщо ~n=5~, то будуть дороги ~(1, 2)~, ~(2, 4)~, ~(3, 1)~, ~(4, 3)~, ~(5, 5)~.

З'ясуйте, чи з кожного міста можна потрапити у будь-яке інше місто, рухаючись дорогами. Якщо ні, то знайдіть пару міст, які не з'єднані.

Формат вхідних даних

Перший рядок містить одне ціле число ~n~ (~1 \leq n \leq 10^6~).

Формат вихідних даних

Виведіть ~YES~, якщо з кожного міста можна потрапити у будь-яке інше місто.

Інакше, у першому рядку виведіть ~NO~. У другому рядку виведіть будь-які два міста ~a~ та ~b~ (~1 \leq a, b \leq n~; ~a \neq b~) такі, що з міста ~a~ неможливо потрапити у ~b~, рухаючись дорогами.

Приклад вхідних даних

5

Приклад вихідних даних

NO
1 5

Приклад вхідних даних

4

Приклад вихідних даних

YES

Приклад вхідних даних

7

Приклад вихідних даних

NO
1 7

Приклад вхідних даних

8

Приклад вихідних даних

YES

Андрійко напився дуже багато компотику, і тепер він дуже боїться прямокутників. Кімнату Андрійка можна математично представити як прямокутник висотою ~n~ і шириною ~m~. У цій кімнаті є ~k~ прямокутників, кожен з яких повністю лежить у кімнаті й не торкається точок ~(0,0)~ та ~(n,m)~, точка ~(0,0)~ - ліва верхня, ~(n,m)~ - права нижня.

Андрійко хоче прийти з кута ~(0,0)~ в кут ~(n,m)~, жодного разу не опиняючись у жодному з ~k~ прямокутників (навіть не торкаючись їх). Якщо він перебуває в координаті ~(x, y)~, то за один крок він може переміститися у будь-яку з наступних координат: ~(x-0.5, y)~, ~(x+0.5, y)~, ~(x, y-0.5)~, ~(x, y+0.5)~, але лише за умови, що наступна координата не виходить за межі прямокутника.

Визначте, чи зможе він дійти від одного кута до іншого.

Формат вхідних даних

Перший рядок містить три цілі числа ~n~, ~m~, ~k~ ~(1 \le n,m \le 10^6, 1 \le k \le 5\,000)~

Кожен з наступних ~k~ рядків містить чотири цілі числа ~x_1~, ~y_1~, ~x_2~, ~y_2~ ~(0 \le x_1 \le x_2 \le n; 0 \le y_1 \le y_2 \le m)~ --- координати верхнього лівого та правого нижнього кутів прямокутника ~i~.

Гарантується, що жоден прямокутник не дотикається до точок ~(0,0)~ та ~(n, m)~.

Формат вихідних даних

Виведіть ~YES~, якщо Андрійко може пройти між кінцями кімнати, і ~NO~ --- інакше.

Оцінювання

• (~3~ бали): ~k = 1~
• (~4~ бали): ~k = 2~
• (~5~ балів): ~k = 3~
• (~17~ балів): ~1 \le k \le 50~
• (~26~ балів): ~1 \le k \le 1000~
• (~20~ балів): ~1 \le n,m \le 5000~
• (~25~ балів): Без додаткових обмежень

Приклад вхідних даних

3 4 3
0 2 1 4
1 2 3 3
2 1 3 3

Приклад вихідних даних

NO

Приклад вхідних даних

3 4 3
0 2 1 4
1 0 2 1
2 1 3 3

Приклад вихідних даних

YES

Дано масив ~a~ довжиною ~n~. Ціна підмасиву --- це добуток довжини підмасиву на суму двох найменших чисел.

Підмасив ~a[l..r]~ --- це частина масиву ~a~, якщо брати до уваги лише числа, що знаходяться на позиціях від ~l~ до ~r~ включно.

Наприклад, нехай дано масив ~[5, 3, 1, 5, 3]~. Розглянемо підмасив ~a[2..4]~, елементи (~a[2..4]~) --- ~[3, 1, 5]~. Його довжина --- ~3~, перший мінімум --- ~1~, другий мінімум --- ~3~. Виходить, що його ціна --- ~3 \cdot (1 + 3) = 12~. Розглянемо інший підмасив ~a[1..2]~, елементи (~a[1..2]~) --- ~[5, 3]~. Його довжина --- ~2~, перший мінімум --- ~3~, другий мінімум --- ~5~. Виходить, що його ціна ~2 \cdot (3 + 5) = 16~.

Зверніть увагу, що якщо мінімальне число трапляється більше одного разу, то воно все одно рахується кілька разів. Наприклад, якщо є підмасив ~[3, 1, 1]~, то його довжина --- ~3~, перший мінімум --- ~1~, другий мінімум --- ~1~. Тобто його ціна --- ~3 \cdot (1 + 1) = 6~.

Ваше завдання --- знайти максимальну ціну щодо всіх підмасивів довжини, як мінімум, два елементи. Тобто потрібно знайти максимальну ціну за всіма підмасивами ~a[l..r]~, де (~1 \leq l < r \leq n~).

Оцінювання

• (~6~ бали): ~2 \le n \le 800~
• (~7~ бали): ~2 \le n \le 5\,000~
• (~10~ балів): ~2 \le n \le 20\,000~
• (~24~ балів): Усі тести згенеровано рандомно наступним чином: спершу визначається число ~n~, що відбувається не рандомно, а потім для кожного ~a_i~ (~1 \le i \le n~ ) присвоюється значення від ~1~ до ~10^9~ включно з однаковою ймовірністю для кожного значення. ~2 \le n \le 10^5~.
• (~17~ балів): ~2 \le a_i \le \sqrt{n}~
• (~36~ балів): Без додаткових обмежень

Формат вхідних даних

Перший рядок містить одне ціле число ~n~ ~(2 \le n \le 10^6)~.

Другий рядок містить ~n~ цілих чисел ~a_1, a_2, \dots, a_n~ ~(1 \le a_i \le 10^9)~.

Формат вихідних даних

Виведіть одне ціле число --- відповідь на задачу.

Примітка

У першому прикладі максимум досяжний на підмасиві ~a[1..5]~, його довжина ~5~, мінімуми --- ~1~ i ~3~, добуток ~(1+3) \cdot 5 = 20~.

У другому прикладі максимум досяжний на підмасиві ~a[5..6]~, його довжина ~2~, мінімуми --- ~10~ i ~77~, добуток ~(10+77) \cdot 2=174~.

У третьому прикладі максимум досяжний на підмасиві ~a[2..3]~, його довжина ~2~, мінімуми --- ~2~ i ~3~, добуток ~(2+3) \cdot 2=10~.

Приклад вхідних даних

5
5 3 1 5 3

Приклад вихідних даних

20

Приклад вхідних даних

7
1 1 3 5 10 77 5

Приклад вихідних даних

174

Приклад вхідних даних

3
1 2 3

Приклад вихідних даних

10