Степан проводить змагання з ~N~ гравцями, пронумерованими від 1 до ~N~. Гравці змагатимуться за очки. Наразі всі гравці мають нуль очок.

Здатність Степана передбачати дозволяє йому знати, як зміняться результати гравців. Зокрема, для ~i=1,2,…,T~ рахунок гравця ~A_i~ ​ збільшиться на ~B_i~ ​ очок через ~i~ секунд. Інших змін у балах не буде.

Степан, який віддає перевагу різноманітності в балах, хоче знати, скільки різних значень балів зʼявлятиметься серед результатів гравців у кожен момент. Для кожного ~i=1,2,…,T~ знайдіть кількість різних значень очок серед очок гравців на ~i + 0,5~ секунді.

Наприклад, якщо в певний момент гравці мають 10, 20, 30 і 20 очок, серед результатів гравців на цей момент є три різні значення.

Обмеження

• ~1≤N,T≤2×10^5~
• ~1≤A_i ≤N~
• ~1≤B_i ≤10^9~
• Усі вхідні значення є цілими числами

Формат вхідних даних

Перший рядок містить цілі числа ~N,T~.

Наступні  ~T~ рядків містять цілі числа ~A_i, B_i~.

Формат вихідних даних

У вихідний потік виведіть ~Т~ рядків.

~i~-й рядок (~1≤i≤T~) має містити ціле число - кількість різних значень очок серед очок гравців на ~i + 0,5~ секунді.

Приклад вхідних даних

3 4
1 10
3 20
2 10
2 10

Приклад вихідних даних

2
3
2
2

Нехай ~S~ буде послідовністю очок гравців 1, 2, 3 у такому порядку. Наразі ~S=\{0,0,0\}~.

• Через одну секунду рахунок гравця 1 збільшується на 10 очок і ~S=\{10,0,0\}~. Таким чином, через 1,5 секунди серед результатів гравців є два різні значення.
• Через дві секунди рахунок гравця 3 збільшується на 20 очок і ~S=\{10,0,20\}~. Таким чином, через 2,5 секунди серед результатів гравців є три різні значення.
• Через три секунди рахунок гравця 2 збільшується на 10 очок і ~S=\{10,10,20\}~. Таким чином, через 3,5 секунди серед результатів гравців є два різні значення.
• Через чотири секунди рахунок гравця 2 збільшується на 10 очок і ~S=\{10,20,20\}~. Таким чином, через 4,5 секунди серед результатів гравців є два різні значення.

Приклад вхідних даних

1 3
1 3
1 4
1 3

Приклад вихідних даних

1
1
1

Приклад вхідних даних

10 10
7 2620
9 2620
8 3375
1 3375
6 1395
5 1395
6 2923
10 3375
9 5929
5 1225

Приклад вихідних даних

2
2
3
3
4
4
5
5
6
5

Вам надано послідовність ~A=(A_1 ​ ,A_2 ​ ,…,A_N ​ )~ довжини ~N~.

Обробіть ~Q~ запитів у тому порядку, у якому вони надані. Кожен запит належить до одного з наступних двох типів:

• Тип 1: 1 p x. Змініть значення ~A_p~ ​ на ~x~.
• Тип 2: 2 l r. Виведіть кількість входжень другого за величиною значення в (~A_l ​,A_{l+1} ​ ,…,A_r ​)~. Точніше, виведіть кількість цілих чисел ~i~, які задовольняють ~l≤i≤r~ так, що серед ~A_l ​,A_{l+1} ,…,A_r~ ​ існує рівно одне окреме значення, більше за ~A_i~ ​.

Обмеження

• ~1≤N,Q≤2×10^5~
• ~1≤A_i ​ ≤10^9~
• Для запитів типу 1 ~1≤p≤N~.
• Для запитів типу 1 ~1≤x≤10^9~.
• Для запитів типу 2, ~1≤l≤r≤N~.
• Є принаймні один запит типу 2.
• Усі вхідні значення є цілими числами.

Формат вхідних даних

Перший рядок містить цілі числа ~N,Q~.

Наступний   рядок містить ~N~ цілих чисел ~A_i~.

Наступні  ~Q~ рядків містять запити описаних типів.

Формат вихідних даних

Нехай ~q~ буде кількістю запитів типу 2.

Вивести ~q~ рядків. ~I~-й рядок має містити відповідь на ~i~-й запит 2-го типу.

Приклад вхідних даних

5 4
3 3 1 4 5
2 1 3
2 5 5
1 3 3
2 2 4

Приклад вихідних даних

1
0
2

Спочатку A=(3,3,1,4,5).

• Для першого запиту другим найбільшим значенням у (3,3,1) є 1, яке зʼявляється один раз у 3,3,1, тому виведіть 1.
• Для другого запиту в (5) немає другого найбільшого значення, тому виведіть 0.
• Третій запит створює A=(3,3,3,4,5).
• Для четвертого запиту другим найбільшим значенням у (3,3,4) є 3, яке зʼявляється двічі в 3,3,4, тому надрукуйте 2.

Приклад вхідних даних

1 1
1000000000
2 1 1

Приклад вихідних даних

0

Приклад вхідних даних

8 9
2 4 4 3 9 1 1 2
1 5 4
2 7 7
2 2 6
1 4 4
2 2 5
2 2 7
1 1 1
1 8 1
2 1 8

Приклад вихідних даних

0
1
0
2
4

Вам надано ~N~ рядків ~S_1 ​ , S_2 ​ ,…, S_N ~.

Знайдіть мінімальну довжину рядка, який містить усі ці рядки як підрядки.

Тут рядок ~S~ містить рядок ~T~ як підрядок, якщо ~T~ можна отримати шляхом видалення нуля або більше символів з початку та нуля або більше символів з кінця ~S~.

Обмеження

• ~N~ є цілим числом.
• ~1≤N≤20~
• ~S_i~ ​ — це рядок, що складається з малих англійських літер, довжина яких дорівнює принаймні 1.
• Загальна довжина ~S_1 ​,S_2 ​,…,S_N~ ​ становить не більше ~2×10^5 ~.

Формат вхідних даних

Перший рядок містить ціле число ~N~.

Наступні  ~N~ рядків містять ~S_i~.

Формат вихідних даних

У вихідний потік виведіть відповідь - одне ціле число.

Приклад вхідних даних

3
snuke
kensho
uk

Приклад вихідних даних

9

Рядок snukensho довжиною 9 містить усі ~S_1 ​, S_2~ ​ і ~S_3~ ​ як підрядки.

Зокрема, символи з першого по пʼятий snukensho відповідають ~S_1~ ​, з четвертого по девʼятий – ~S_2~ ​, а з третього по четвертий – ~S_3~ ​.

Жоден коротший рядок не містить усі ~S_1 ​, S_2~ ​ і ~S_3~ ​ як підрядки. Отже, відповідь 9.

Приклад вхідних даних

3
abc
abc
arc

Приклад вихідних даних

6

Приклад вхідних даних

6
cmcmrcc
rmrrrmr
mrccm
mmcr
rmmrmrcc
ccmcrcmcm

Приклад вихідних даних

27

На площині є коло. Воно містить ~N~ різних точок, пронумерованих ~1,2,…,N~ за годинниковою стрілкою.

Існує ~ \frac{N(N-1)}{2}~ ​ відрізків, які можна побудувати, зʼєднавши дві різні точки серед ~N~ точок. Треба побудувати M із цих відрізків.

Знайдіть кількість способів побудови ~M~ відрізків так, щоб жодні два з них не перетиналися в точці, відмінній від кінцевих. Відповідь вивести за модулем ~10^9+7~.

Обмеження

• ~1≤N≤10^7~
• ~0≤M≤ \frac{N(N-1)}{2}~ ​

Формат вхідних даних

Вхідний потік містить цілі числа ~N, M~.

Числа розділяються пропуском.

Формат вихідних даних

У вихідний потік виведіть відповідь.

Приклад вхідних даних

4 2

Приклад вихідних даних

14

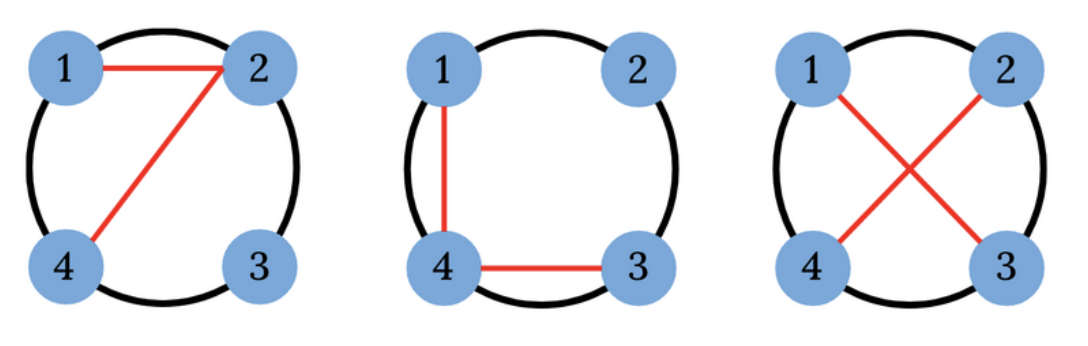
Наступні приклади ліворуч і посередині задовольняють умови. (Зауважте, що допустимо, щоб відрізки перетиналися в своїх кінцевих точках.)

Приклад праворуч не підходить, оскільки два ребра перетинаються в точці, відмінній від їхніх кінцевих точок.

Приклад вхідних даних

6 3

Приклад вихідних даних

295

Приклад вхідних даних

2023 1217

Приклад вихідних даних

10811951