В лабораторії досліджують дію випромінювань на рослини при опроміненні через силові поля.

Експериментальна установка має квадратну платформу розміром ~10^9*10^9~, заповнену грунтом. Над платформою встановлене джерело випромінювання. Між джерелом випромінення і платформою можна вмикати ~N~ силових полів.

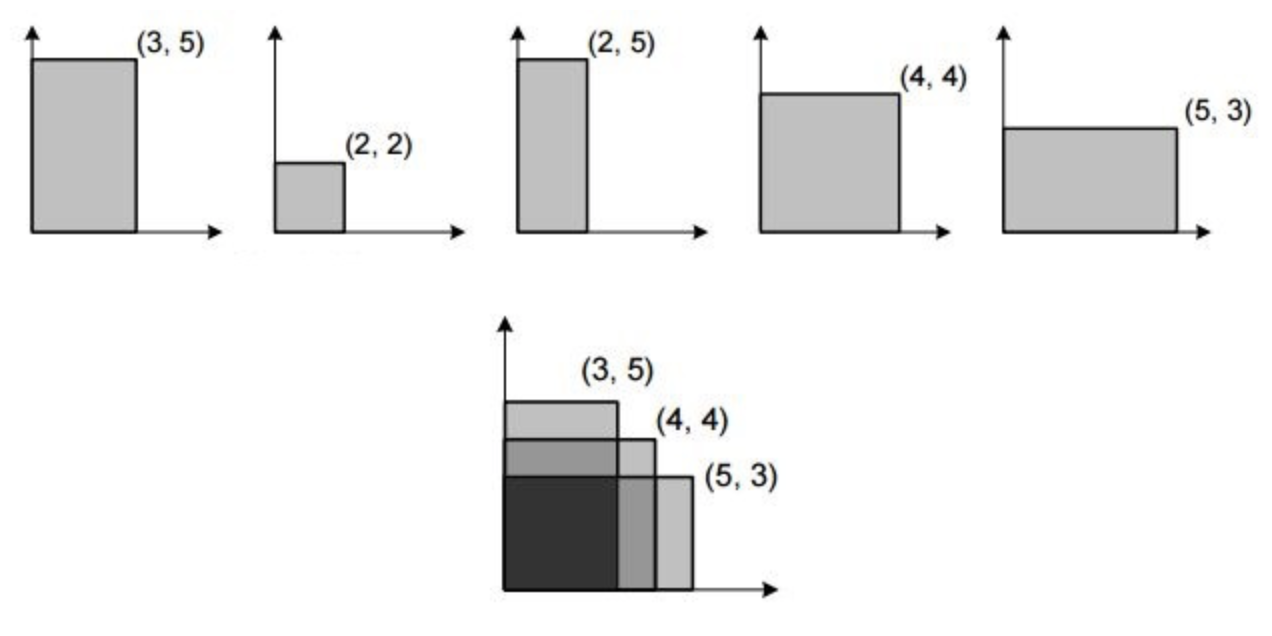
Генератор силового поля встановлений над точкою (0,0).При цьому i-те силове поле, представляє собою прямокутник зі сторонами паралельними границям платформи, і координатами двох протилежних кутів (0,0) та (~X_i,Y_i~).

В експерименті планується вивчити дію ~K~ силових полів. З заданих ~N~ полів необхідно обрати ~K~ полів для експеримента. Вчені хочуть обрати поля таким чином, щоб площа ділянки платформи, над якою знаходяться ВСІ ~K~ обраних полів, була максимальна

Виведіть максимально можливу площу ділянки.

Формат вхідних даних

Перший рядок містить два цілих числа ~N,K~ (~1 \le K \le N \le 200000~) - загальна кількість силових полів, і кількість полів яку необхідно обрати.
Наступні ~N~ рядків містять по 2 цілих числа ~X_i,Y_i~ (~1 \le X_i, Y_i \le 10^9~) - координати дальнього від початку координат кута відповідної ділянки силового поля

Підзадачі:
20% - (~1 \le N \le 20~) , (~1 \le K \le N~)
20% - (~1 \le N \le 300~) , (~1 \le K \le N~)
20% - (~1 \le N \le 3000~) , (~1 \le K \le N~)
20% - (~2 \le N \le 200000~) , (~K=2~)
20% - (~1 \le N \le 200000~) , (~1 \le K \le N~)

Формат вихідних даних

Виведіть відповідь на задачу

Приклад вхідних даних-1

5 3
3 5
2 2
2 5
4 4
5 3

Приклад вихідних даних-1

9

Темні сили під керівництвом Саурона заполонили Середзем'я, і лише Арагорн, син Араторна, спадкоємець Ісілдура та справжній правитель Гондору, може знайти сили протистояти Темному володарю Мордору. Втім, йому ми допоможемо іншим разом, зараз же давайте оцінимо, як далеко може зайти Темний Володар.

Карта Середзем'я є картатий прямокутник з ~N~ рядків по ~M~ клітин, кожна з яких може або повністю належати Саурону, або повністю не належати. Якщо у будь-якому квадраті розміром 2 × 2 три клітини вже захоплені темними силами, вони можуть завоювати четверту клітину цього квадрата.

Спочатку полчищам Саурона підвладна кілька клітин карти Середзем'я. Оцініть максимальну кількість клітин, які можуть підвести під його контроль.

Формат вхідних даних

У першому рядку містяться два цілих числа ~N~ і ~M~ ( ~1 ≤ N , M ≤ 1 000~ ) — кількість рядків і стовпців на карті Середзем'я.

Наступні ~N~ рядків по ~M~ символів описують клітини карти. Символ ' . ' відповідає клітці карти, вільної від влади Саурона, а '#' - клітці, захопленої Сауроном. Рядки нумеруються від 1 до ~N~, стовпці - від 1 до ~M~.

Формат вихідних даних

Виведіть одне число - максимальну кількість клітин, які можуть контролювати темні сили після всіх завоювань.

Приклад вхідних даних

2 2
##
#.

Приклад вихідних даних

4

Приклад вхідних даних

3 4
#...
#...
###.

Приклад вихідних даних

9

Приклад вхідних даних

3 5
...##
#....
#.#..

Приклад вихідних даних

5

У нових елітних електричках кожному пасажиру відведено сидяче місце. Звичайно, кількість сидячих місць обмежена і на всіх їх може не вистачити.

Маршрут електрички проходить через ~N+1~ станцію. Станції пронумеровані від 0 до ~N~. Коли людина хоче купити квиток, він називає два числа ~x~ та ~y~ – номери станцій, звідки і куди він хоче їхати. За наявності хоча б одного місця сидіння на цій ділянці на момент покупки йому продається квиток, інакше видається повідомлення «квитків немає» і квиток не продається.

Ваше завдання – написати програму, яка обслуговує такі запити в порядку їх приходу.

Формат вхідних даних

У першому рядку містяться три числа ~N~ – кількість станцій (~1 ≤ N ≤ 200 000~), ~K~ – кількість місць в електричці (~1 ≤ K ≤ 1000~) та ~M~ – кількість запитів (~1 ≤ M ≤ 100 000)~.

У наступних ~M~ рядках описані запити, кожен із яких складається з двох чисел ~x~ та ~y~ (~0 ≤ x < y \le N~).

Формат вихідних даних

На кожен запит ваша програма повинна видавати результат у вигляді числа 0, якщо квиток не продається і 1, якщо квиток був проданий. Кожен результат має бути на окремому рядку

Оцінювання

• 30%, ~N,M \le 10000~, тести 1-8
• 70%, без додаткових обмежень, тести 9-17

Приклад вхідних даних

5 2 4
0 4
1 2
1 4
2 4

Приклад вихідних даних

1
1
0
1

На вокзалі є ~K~ глухих кутів, куди прибувають електрички. Цей вокзал є їхньою кінцевою станцією, тому електрички, прибувши, деякий час стоять на вокзалі, а потім вирушають у новий рейс (у той бік, звідки прибули).

Дано розклад руху електричок, в якому для кожної електрички вказано час її прибуття, а також відправлення в наступний рейс. Електрички у розкладі впорядковані за часом прибуття. Оскільки вокзал — кінцева станція, то електричка може стояти на ньому досить довго, зокрема, електричка, яка прибуває раніше за іншу, вирушати назад може значно пізніше.

Тупики пронумеровані числами від 1 до ~K~. Коли електричка прибуває, її ставлять у вільний глухий кут з мінімальним номером. При цьому якщо електричка з якогось глухого кута вирушила в момент часу ~X~, то електричку, яка прибуває в момент часу ~X~, в цей глухий кут ставити не можна, а електричку, що прибуває в момент ~X+1~ - можна.

Напишіть програму, яка за даним розкладом для кожної електрички визначить номер глухого кута, куди прибуде ця електричка.

Формат вхідних даних

Спочатку вводяться число ~K~ - кількість тупиків і число ~N~ - кількість електропоїздів (~1≤K≤100000~, ~1≤N≤100000~).

Далі слідують ~N~ рядків, у кожному з яких записано по 2 числа: час прибуття та час відправлення електрички. Час задається натуральним числом, що не перевищує ~10^9~. Ніякі дві електрички не прибувають в один і той же час, але при цьому кілька електричок можуть вирушати в один і той же час. Також можливо, що якась електричка (або навіть кілька) вирушають у момент прибуття якоїсь іншої електрички. Час відправлення кожної електрички строго більший за час її прибуття.

Усі електрички впорядковані за часом прибуття. Вважається, що в нульовий момент часу всі тупики на вокзалі вільні.

Формат вихідних даних

Виведіть ~N~ чисел - по одному для кожної електрички: номер глухого кута, куди прибуде відповідна електричка. Якщо тупиків недостатньо для того, щоб організувати рух електричок згідно з розкладом, виведіть два числа: перше має дорівнювати 0 (нулю), а друге містити номер першої з електричок, яка не зможе прибути на вокзал.

Оцінювання

• 20%, ~K,N \le 10~, тести 1-8
• 20%, ~K,N \le 1000~, тести 9-11
• 60%, без додаткових обмежень, тести 9-17

Приклад вхідних даних

1 1
2 5

Приклад вихідних даних

1

Приклад вхідних даних

1 2
2 5
5 6

Приклад вихідних даних

0 2

Приклад вхідних даних

2 3
1 3
2 6
4 5

Приклад вихідних даних

1
2
1

Власники рибальського судна, що веде промисел на річці Кама, вирішили у літньому сезоні оптимізувати свій бізнес.

Вони отримали сезонний дозвіл на лов риби в ~n~ точках русла річки на відстанях ~x_1,x_2,…,x_n~ кілометрів від гирла. При цьому в точці з номером ~i~ дозволяється виловити не більше ~a_i~ тонн риби.

Виловлену рибу можна продавати на ~m~ оптових базах, розташованих уздовж берега річки в точках на відстанях ~y_1, y_2,…, y_m~ км від гирла. При цьому база в точці номер ~𝑗~ готова цього сезону закупити не більше ~𝑏_𝑗~ тонн риби за ціною ~𝑐_𝑗~ за тонну.

Відстані від гирла до точок вилову та оптових баз вимірюються вздовж русла річки.

Судно вирушає на лов із гирла річки і має повернутися туди ж після закінчення сезону. Протягом сезону судно може довільним чином плавати вгору та вниз по річці, зупиняючись для лову чи продажу риби. Вантажопідйомність судна достатня для перевезення будь-якої кількості виловленої риби. При віддаленні від гирла судно рухається проти течії, витрачаючи на один кілометр шляху паливо вартістю ~𝑝~. При переміщенні у бік гирла судно рухається за течією і тому не витрачає палива.

За підсумками сезону прибуток за улов дорівнюватиме сумарній вартості проданої риби за вирахуванням сумарної вартості витраченого палива.

Потрібно написати програму, яка визначає максимальний прибуток, який можна отримати за сезон.

Формат вхідних даних

Перший рядок вхідних даних містить три цілих числа ~𝑛, 𝑚~ і ~𝑝~ - кількість точок лову риби, кількість оптових баз і вартість палива (~1≤𝑛,𝑚≤500000~;~0≤𝑝≤10^9~).

Наступні ~𝑛~ рядків містять по два цілих числа ~𝑥_𝑖~ і ~𝑎_𝑖~ - відстань від гирла і максимальний улов для кожної точки лову риби ~(0<𝑥_1<𝑥_2<⋯<𝑥_𝑛≤10^9~;~0<𝑎_i \le 10^6)~

Наступні ~𝑚~ рядків містять по три цілих числа ~𝑦_𝑗,𝑏_𝑗,𝑐_𝑗~ - відстань від гирла, максимальна кількість тонн риби, що закуповується, і ціна закупівлі за тонну для кожної оптової бази ~(0<𝑦_1<𝑦_2<⋯< 𝑗_m ≤10^6~, ~0<𝑏_𝑗,𝑐_𝑗≤10^6~).

Формат вихідних даних

Вихідні дані мають містити єдине ціле число — максимальний можливий прибуток.

Пояснення до прикладів

У другому прикладі оптимальними будуть такі дії. Слід доплисти до точки на відстані 6 кілометрів від гирла, витративши 600 на паливо, та виловити у ній 5 тонн риби. Після цього слід спуститися на 1 кілометр річкою до бази на відстані 5 кілометрів від гирла і продати виловлену рибу за ціною 2000 за тонну. Потім слід повернутися у гирло річки. Сумарний прибуток становитиме 9400.

Приклад вхідних даних

3 2 0
1 5
2 3
4 5
2 2 10
3 6 5

Приклад вихідних даних

50

Приклад вхідних даних

2 1 100
6 5
100 4
5 100 2000

Приклад вихідних даних

9400

Приклад вхідних даних

3 3 10
1 1
10 100
20 10
2 1000 1
11 50 50
17 50 2

Приклад вихідних даних

2441