Дано шахiвниця розмiром ~n × m~. Тобто з ~n~ рядками та ~m~ стовпчиками.

У цiй шахiвницi є лише одна фiгура — тура. Вона знаходиться у нижньому лiвому кутi. Бiльше нiяких фiгур немає.

Нагадаємо, що тура за один хiд може перемiститися на будь-яку кiлькiсть клiтин по горизонталi або вертикалi, але не по дiагоналi.

Знайдiть кiлькiсть клiтин, на якi тура може перемiститися за один хiд.

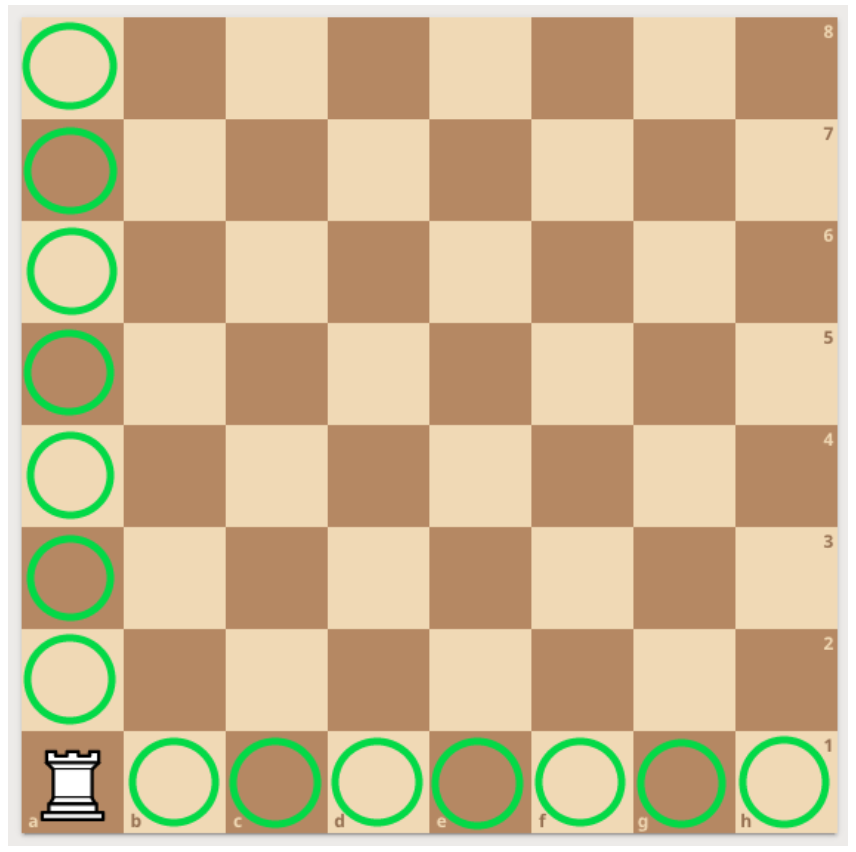
На малюнку зображена традицiйна шахiвниця розмiру 8 × 8. У нiй тура може перемiститися на всi клiтини, якi помiченi зеленим. Таких всього 14, тому вiдповiдь 14.

Формат вхiдних даних

Перший рядок мiстить одне цiле число ~n~ (~1 \le n \le 20~).

Другий рядок мiстить одне цiле число ~m~ (~1 \le m \le 20~).

Формат вихiдних даних

Виведiть кiлькiсть клiтин, на якi тура може перемiститися за один хiд.

Приклад вхідних даних

8
8

Приклад вихідних даних

14

Приклад вхідних даних

3
2

Приклад вихідних даних

3

Пояснення, чому до першого прикладу вiдповiдь 14, можна побачити на малюнку вище.

У другому прикладi вiдповiдь 3, бо тура може перемiститися лише на одну позицiю вгору та на двi позицiї вправо.

Дана кiмната розмiром ~n × m~.

Знайдiть максимальну кiлькiсть цiлих плиток розмiром ~k × k~, якi можна помiстити у кiмнатi?

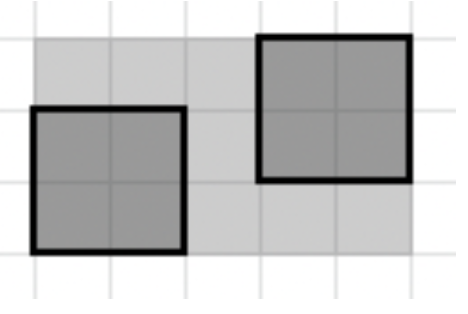
На малюнку зображена одна з можливих максимальних вiдповiдей для ~n~ = 5, ~m~ = 3, ~k~ = 2.

Формат вхiдних даних

Перший рядок мiстить цiле число ~n~ (~1 \le n \le 1000~).

Другий рядок мiстить цiле число ~m~ (~1 \le m \le 1000~).

Третiй рядок мiстить цiле число ~k~ (~1 \le k \le 1000~).

Формат вихiдних даних

Виведiть одне цiле число — вiдповiдь на задачу.

Приклад вхідних даних

5
3
2

Приклад вихідних даних

2

Андрiй не полюбляє рiзкi перепади, а особливо в контестах. Два числа ~a~ i ~b~ утворюють рiзкий перепад, якщо ~|a - b|~ > 1. Скажемо, що контест є плавним, якщо нiякi складностi двох сусiднiх задач не утворюють рiзкий перепад. Вам дано 5 чисел — складностi задач. Визначте, чи утворюють цi задачi плавний контест.

Формат вхiдних даних

Перший рядок мiстить пʼять цiлих чисел ~a~, ~b~, ~c~, ~d~, ~e~ (~1 \le a, b, c, d, e \le 10^6~) — складностi задач.

Формат вихiдних даних

Виведiть «Yes», якщо числа утворюють плавний контест, i «No» в iншому випадку.

Приклад вхідних даних

1 2 2 2 1

Приклад вихідних даних

Yes

Приклад вхідних даних

1 2 2 1 3

Приклад вихідних даних

No

Зауваження

Пояснення до першого прикладу: |1 - 2| = 1, |2 - 2| = 0, |2 - 2| = 0, |2 - 1| = 1. Жодна з цих пар не утворює рiзкий перепад, тому числа 1, 2, 2, 2, 1 утворюють плавний контест. Пояснення до другого прикладу: |1 - 2| = 1, |2 - 2| = 0, |2 - 1| = 1, |1 - 3| = 2. Як можна бачити, останнi два числа утворюють рiзкий перепад, тому числа 1, 2, 2, 1, 3 не утво- рюють плавний контест.

В Антона був масив ~A~ i вiн його дуже любив. Вiн знає декiлька фактiв про цей масив:

• Сума елементiв даного масиву — парне число
• Для будь-якого ~i~ (~1 \le i < |A|~) виконується ~A_i \le A_{i+1}~, де ~|A|~ — розмiр масиву ~A~.
• ~0 \le A_i \le 1~.
• ~A_i~ — цiле число.

Один раз, повертаючись додому, Антон помiтив злого Грандi поряд зi своїм масивом. Вiн мiг вкрасти один елемент з масиву ~A~. Вам дано масив ~B~ — масив, який був, коли Антон прийшов додому.

Знайдiть кiлькiсть способiв додати не бiльше одного елементу до масиву ~B~, щоб вийшов масив, який задовольняє умовам вище.

Формат вхiдних даних

Перший рядок мiстить одне цiле число ~n~ (~1 \le n \le 10^5~) — кiлькiсть елементiв масиву ~B~.

Другий рядок мiстить ~n~ цiлих чисел ~B_i~ (~0 \le B_i \le 1~).

Формат вихiдних даних

Виведiть одне цiле число — вiдповiдь на задачу.

Приклад вхідних даних

1
0

Приклад вихідних даних

3

Приклад вхідних даних

1
1

Приклад вихідних даних

2

Приклад вхідних даних

2
1 0

Приклад вихідних даних

0

Приклад вхідних даних

5
0 0 0 1 1

Приклад вихідних даних

5

Приклад вхідних даних

7
0 0 0 0 1 1 1

Приклад вихідних даних

4

Зауваження

Пояснення до першого прикладу:

Якщо нiчого не додавати вийде A = [0], що задовольняє умовам.

Якщо додати 0 в початок масиву вийде A = [0, 0], що задовольняє умовам.

Якщо додати 1 в початок масиву вийде A = [1, 0], що не задовольняє умовам.

Якщо додати 0 в кiнець масиву вийде A = [0, 0], що задовольняє умовам.

Якщо додати 1 в кiнець масиву вийде A = [0, 1], що не задовольняє умовам.

Пояснення до пʼятого прикладу:

Умови задовольняють наступнi масиви [0,0,0,0, 1,1,1,1], [0,0,0,0,1, 1,1,1], [0,0,0,0,1,1, 1,1], [0,0,0,0,1,1,1,1].

Андрiй, як справжнiй цукеркоман, коли приходить в магазин купляє все, що бачить. А саме, у кожний свiй вiзит вiн купляє цукерки з послiдовними номерами вiд ~l~ до ~r~.

Завтра Андрiй вирушає на дуже вiдповiдальний захiд — фiнал ВЮДОI, а тому хоче взяти з собою як можна бiльше цукерок. Вiн знає, що цукерка з номером ~i~ важить ~i~ грамiв, а його рюкзак може витримувати вагу до ~w~ грамiв. Всього було ~n~ вiзитiв до магазину, в кожен з яких вiн може придбати цукерки з iнтервалу ~[l_i,r_i]~.

Скажiть максимальну кiлькiсть цукерок, яку вiн може взяти з собою, якщо вiдомо, що вiн може брати не бiльше ~i~ цукерок з номером ~i~.

Формат вхiдних даних

Перший рядок мiстить два цiлi числа ~n~ (~1 \le n \le 10^6~) та ~w~ (~1 \le w \le 10^{12}~) — кiлькiсть вiзитiв до магазину та максимальна вага, яку може витримати рюкзак Андрiя у грамах.

Наступнi ~n~ рядкiв мiстять кожен по два цiлi числа ~l_i~ та ~r_i~ (~1 \le l_i \le r_i \le 10^5~).

Формат вихiдних даних

Виведiть одне цiле число — вiдповiдь на задачу.

Приклад вхідних даних

3 14 
1 4
2 3 
4 5

Приклад вихідних даних

5

Приклад вхідних даних

3 20
1 10
1 10
1 10

Приклад вихідних даних

7

Зауваження

Пояснення до першого прикладу:

Список усiх цукерок, якi купив Андрiй — [1, 2, 3, 4, 2, 3, 4, 5].

Один з варiантiв взяти 5 цукерок — [2, 3, 4, 3, 2].

Пояснення до другого прикладу:

Один з варiантiв взяти 7 цукерок буде наступним — [1, 2, 2, 3, 3, 4, 5], сумарна вага буде 20 грамiв.