1479: Дві матриці
Перегляд у форматі PDFЗадано двi квадратнi матрицi ~А~ та ~В~ однакової розмiрностi. До матрицi ~А~ можна нескiнченну кiлькiсть разiв застосувати наступнi дiї:
Взяти будь-яку її квадратну пiдматрицю
Транспонувати її (замiнити її рядки на стовпчики)
Потрiбно визначити чи можна такими дiями iз матрицi ~А~ отримати матрицю ~В~.
Формат вхідних даних
В першому рядку задається кiлькiсть вхiдних тестiв ~t~. Кожен тест мiстить розмiр матриць ~n~ та самі матрицi (~n~ рядкiв, що складаються iз ~n~ чисел), елементи яких цiлi додатнi числа, якi не перевищують ~10^6~.
Обмеження:
~1 \le t \le 10~
~2 \le n \le 500~
Формат вихідних даних
Для кожного тесту вивести в окремому рядку вiдповiдь ~Yes~, якщо iз матрицi ~А~ можна одержати матрицю ~В~ або ~No~ в iншому випадку.
Приклад вхідних даних
2
3
1 2 3
4 5 6
7 8 9
1 4 7
2 5 6
3 8 9
2
1 2
3 4
1 4
3 8
Приклад вихідних даних
Yes
No
Зауваження
Для першого тесту, щоб отримати матрицю В, необхiдно спочатку транспонувати всю матрицю, а потiм пiдматрицю з кутами в клiтинках (2, 2) та (3, 3).
Приклад транспонування матрицi:
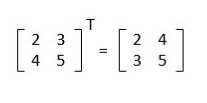
Коментарі