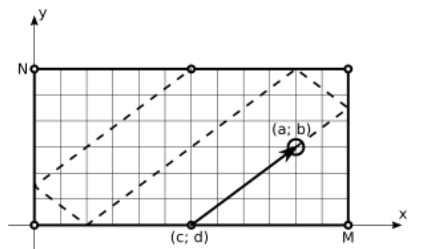
В нас є бiльярдний стiл довжиною ~M~ та шириною ~N~ сантиметрiв. Для спрощення розумiння розмiстимо його на координатнiй площинi таким чином, щоб одна з кутових луз знаходилася в координатах (0; 0), розмiр ~M~ був спрямований вздовж осi ~x~, а розмiр ~N~ був спрямований вздовж осi ~y~. Тодi iншi лузи будуть мати координати ~(M/2; 0)~, ~(M ; 0)~, ~(M ; N )~, ~(M/2; N )~, ~(0; N )~ вiдповiдно.

На столi знаходиться бiльярдна куля в координатах ~(a; b)~ (вимiряних в тих самих сантиметрах). В координатах ~(c; d)~ знаходиться кий, спрямований точно в центр кулi, ~(c; d) \neq (a; b)~. Кий бʼє в кулю, i куля починає рухатися точно в напрямку удару. Тертя вiдсутнє, тому куля рухається з постiйною швидкiстю. Також через вiдсутнiсть тертя куля вiдбивається вiд бортiв точно симетрично, суворо за правилом ʼкут падiння рiвний куту вiдбиванняʼ.

Ця куля могла б рухатися бiльярдним столом вiчно, але. . . вона може попасти в лузу. За даними ~M, N, a, b, c, d~ визначте, чи попаде куля в будь-яку лузу, чи буде рухатися столом вiчно.

~M~ - парне цiле число, ~N, a, b, c, d~ - цiлi числа. ~2 \le M \le 2^{32}~ , ~1 \le N < 2^{32}~ , ~0 \le a \le M ~, ~0 \le b \le N ~, ~0 \le c \le M ~, ~0 \le d \le N ~. Куля i лузи є матерiальними точками, тобто не мають розмiру. Куля попадає в лузу тодi, коли її цiлочисельнi координати точно спiвпадають з цiлочисельними координатами лузи.

Формат вхідних даних

В першому рядку вхiдного потоку мiститься шiсть цiлих чисел, роздiлених довiльною кiлькiстю пропускiв, а саме числа ~M, N, a, b, c, d~ у вказаному порядку.

Формат вихідних даних

В перший рядок вихiдного потоку виведiть єдиний символ «+» (плюс), якщо куля попаде в лузу або символ «-» (мiнус), якщо куля буде рухатися бiльярдним столом вiчно.

Оцінювання

Перші два тести не оцінюються - це тести з умови. Всі інші тести розбитті на пакети, які містять різні варіанти відповіді. Бали нараховуються лише при проходженні всіх тестів з пакету.

Приклад вхідних даних

12 6 7 3 5 5

Приклад вихідних даних

-

Приклад вхідних даних

12 6 10 3 6 6

Приклад вихідних даних

+