1661: Найкоротша відстань
Перегляд у форматі PDFУ деякій країні є ~N~ міст. Між містами є лише дороги з одностороннім рухом - вважається, що таким чином кількість автомобільних пригод мінімізується. Знайдіть найкоротшу відстань, яку треба подолати для того, щоб з міста ~a~ попасти в місто ~b~ описаними дорогами.
Формат вхідних даних
Перший рядок містить два цілих числа ~N~, ~M~ (~2 \le N \le 400~, ~1 \le M \le (n \cdot (n-1))/2~) - кількість міст і кількість доріг відповідно.
Наступні ~M~ рядків містять по три числа ~x~,~y~,~d~ (~1 \le x,y \le N~, ~1 \le d \le 350~), де ~x~ - місто, з якого йде дорога; ~y~ - місто, у яке йде дорога, а ~d~ - довжина дороги.
Наступний рядок містить одне ціле число q (~1 \le q \le 10^5~) - кількість запитів.
Кожен з наступних ~q~ рядків містить по два цілі числа: номер початкового міста і номер кінцевого міста.
З міста до цього ж міста завжди є дорога і довжина її рівна 0.
Якщо від міста ~a~ до міста ~b~ є декілька прямих доріг з різними довжинами, то вважаємо, що є лише одна дорога із довжиною, яка була введена останньою.
Формат вихідних даних
Для кожного запиту вивести довжину найкоротшого шляху з першого міста у друге. У випадку, коли неможливо попасти з першого міста у друге - виведіть -1.
Приклад вхідних даних
4 5
1 2 5
1 4 24
2 4 6
3 4 4
3 2 7
3
1 2
3 1
1 4
Приклад вихідних даних
5
-1
11
Примітка
Ілюстраці до прикладу:
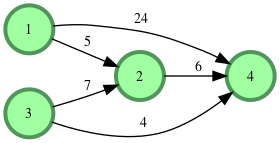
Коментарі
Часу на пайтон вистачає?
Час збільшено, треба шукати більш ефективний алгоритм
Дякую! Оптимізував і все працює.