~L~-knight(~a,b~) може переміститися з клітинки (~x_1,y_1~) в клітинку (~x_2,y_2~) де:

~x_2=x_1 \pm a~ і ~y_2=y_1 \pm b~

або

~x_2=x_1 \pm b~ і ~y_2=y_1 \pm a~

Наприклад, ~L~-knight(1,2) або ~L~-knight(2,1) з червоної клітинки може переміститися в будь-яку зелену.

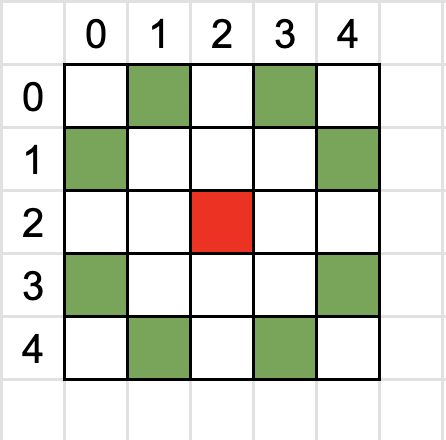
Задається шахівниця розміром ~n \times n~. Дайте відповідь на запитання для кожної пари (~a,b~):

• Яка мінімальна кількість ходів потрібна для ~L~-knight(~a,b~), щоб перейти з позиції (0,0) в позицію (n-1,n-1)? Якщо ~L~-knight(a,b) не може дістатися до місця призначення, то виведіть -1.

Відповідь вивести для кожного ~L~-knight(~a,b~) згідно формату вихідних даних.

Обмеження

• ~5 \le n \le 25~
• ~1 \le a,b \le n~

Формат вхідних даних

Вхідний потік містить одне ціле число ~n~ - розмірність шахівниці.

Формат вихідних даних

У вихідний потік вивести ~n-1~ рядок. ~i~-й (де ~1 \le i \le n~) рядок містить ~n-1~ цілих чисел, розділених пропуском, які є мінімальною кількістю ходів для ~L~-knight(~i,j~) для відповідного ~j~ (де ~1 \le j \le n~) щоб перейти з позиції (0,0) в позицію (n-1,n-1).

Наприклад, для ~n=3~ вихідні дані для всіх пар (~i,j~) розтащуються таким чином:

(1,1) (1,2)
(2,1) (2,2)

Примітка

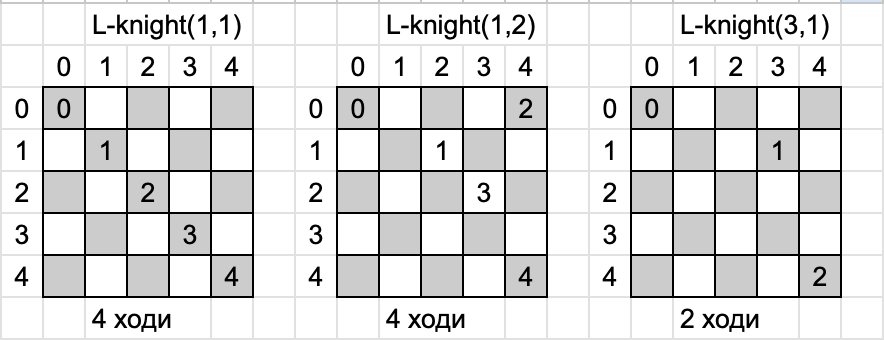
Приклади можливих варіантів ходів для різних ~(i,j)~:

Приклад вхідних даних

5

Приклад вихідних даних

4 4 2 8 
4 2 4 4 
2 4 -1 -1 
8 4 -1 1