Вимірювання земельної ділянки ~-~ важлива геодезична процедура. Щоб отримати точні числові показники, процедуру вимірювання повинні виконувати професійні геодезисти.

Розглянемо таку задачу. Нехай є квадратна ділянка, яку геодезисти розділили на ~n^2~ прямокутних ділянок, провівши ~(n-1)~ вертикальних ліній та ~(n-1)~ горизонтальних ліній. Пронумеруємо стовпчики та рядки діляночок так, як вказано на малюнку (масштабу не дотримано). Тобто рядки нумеруються знизу вгору цілими числами від ~1~ до ~n~; а стовпчики нумеруються зліва направо цілими числами від ~1~ до ~n~.

Ділянки, які знаходяться на перетині ~i~-го стовпчика та ~i~-го рядка ~(1 \le i \le n)~, будемо називати головною діагоналлю. Ділянки, які знаходяться на перетині ~(i+1)~-го стовпчика та ~i~-го рядка ~(1 \le i \le n-1)~, будемо називати побічною діагоналлю.

Вам відомі площі ділянок на головній та побічній діагоналях. Обчисліть площу ділянки, що знаходиться на перетині ~p~-го стовпчика та ~q~-го рядка.

Формат вхідних даних

Перший рядок містить одне ціле число ~n~ (~2 \le n \le 1\,000~).

Другий рядок містить ~n~ цілих чисел ~a_1, a_2, \dots, a_n~ (~1 \leq a_i \leq 10^9~) --- площі ділянок на головній діагоналі.

Третій рядок містить ~n-1~ цілих чисел ~b_1, b_2, \dots, b_{n-1}~ (~1 \leq b_i \leq 10^9~) --- площі ділянок на побічній діагоналі.

Четвертий рядок містить два цілі числа ~p~ та ~q~ (~1 \leq p, q \leq n~) --- координати ділянки, площу якої треба обчислити.

Формат вихідних даних

Виведіть площу ділянки, що знаходиться на перетині ~p~-го стовпчика та ~q~-го рядка.

Ми хочемо знати точне значення площі, тому відповідь треба виводити у факторизованому вигляді. Іншими словами, відповідь треба представити як декілька рядків, кожен з яких містить два цілі числа ~p_i~ та ~s_i~: число ~p_i~ обов'язково просте та всі числа ~p_i~ різні, а число ~s_i~ --- ціле та не дорівнює нулю. Шукана площа має дорівнювати: ~ S = p_1^{s_1} \cdot p_2^{s_2} \cdot p_3^{s_3} \ldots p_k^{s_k}, ~ де ~k~ --- кількість рядків у відповіді. Рядки треба відсортувати за зростанням простих чисел ~p_i~. Нагадаємо, що число ~X~ вважається простим, якщо воно має рівно два цілі додатні дільники: ~1~ та ~X~.

Якщо шукана площа дорівнює 1, то виведіть дві одиниці: 1 1

Оцінювання

• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться на головній або побічній діагоналі. (~p - 1 = q~ або ~p = q~)
• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться на перетині ~i~-го стовпчика та ~(i+1)~-го рядка. (~p + 1 = q~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~10\,000~. Ділянка, площу якої треба обчислити, знаходиться на головній або побічній діагоналі. (~p - 1 = q~ або ~p = q~)
• (~5~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться на головній або побічній діагоналі. (~p - 1 = q~ або ~p = q~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~10\,000~. Ділянка, площу якої треба обчислити, знаходиться на перетині ~i~-го стовпчика та ~(i+1)~-го рядка. (~p + 1 = q~)
• (~5~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться на перетині ~i~-го стовпчика та ~(i+1)~-го рядка. (~p + 1 = q~)
• (~5~ балів): Кількість ділянок дорівнює ~25~ (~n = 5~). Площі всіх відомих ділянок не перевищують ~100~.
• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться у лівому верхньому куті. (~p=1~, ~q=n~)
• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться у правому нижньому куті. (~p=n~, ~q=1~)
• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться над головною діагоналлю. (~p < q~)
• (~5~ балів): Площі всіх відомих ділянок --- прості числа до ~100~ або одиниці. Ділянка, площу якої треба обчислити, знаходиться під головною діагоналлю. (~p > q~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~100~. Ділянка, площу якої треба обчислити, знаходиться у лівому верхньому куті. (~p=1~, ~q=n~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~100~. Ділянка, площу якої треба обчислити, знаходиться у правому нижньому куті. (~p=n~, ~q=1~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~100~. Ділянка, площу якої треба обчислити, знаходиться над головною діагоналлю. (~p < q~)
• (~5~ балів): Площі всіх відомих ділянок не перевищують ~100~. Ділянка, площу якої треба обчислити, знаходиться під головною діагоналлю. (~p > q~)
• (~5~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться у лівому верхньому куті. (~p=1~, ~q=n~)
• (~5~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться у правому нижньому куті. (~p=n~, ~q=1~)
• (~8~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться над головною діагоналлю. (~p < q~)
• (~7~ балів): Загальні обмеження на площі всіх відомих ділянок. Ділянка, площу якої треба обчислити, знаходиться під головною діагоналлю. (~p > q~)

Пояснення

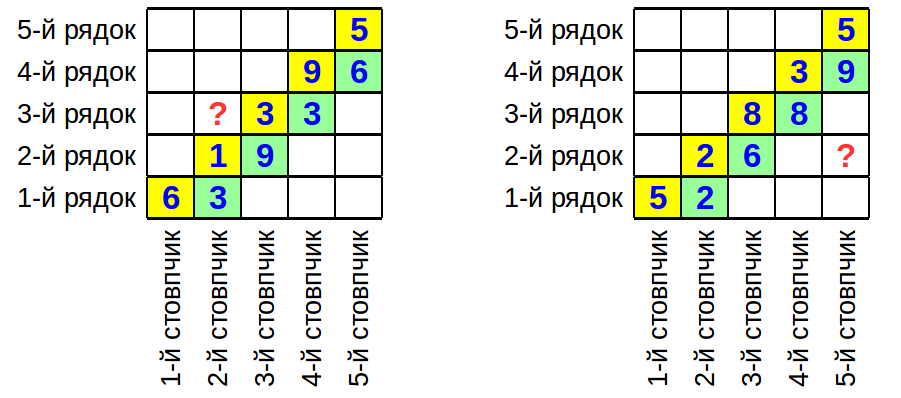
Ділянка, що знаходиться на малюнку ліворуч, відповідає першому тесту з умови. Площа ділянки на перетині 2-го стовпчика та 3-го рядка дорівнює: ~ S = 3^{-1} = \frac{1}{3} ~

Ділянка, що знаходиться на малюнку праворуч, відповідає другому тесту з умови. Площа ділянки на перетині 5-го стовпчика та 2-го рядка дорівнює: ~ S = 2^{1} \cdot 3^2 = 18 ~

Приклад вхідних даних

5
6 1 3 9 5
3 9 3 6
2 3

Приклад вихідних даних

3 -1

Приклад вхідних даних

5
5 2 8 3 5
2 6 8 9
5 2

Приклад вихідних даних

2 1
3 2

Приклад вхідних даних

5
6 1 3 9 5
3 9 3 6
2 4

Приклад вихідних даних

1 1