На площині є коло. Воно містить ~N~ різних точок, пронумерованих ~1,2,…,N~ за годинниковою стрілкою.

Існує ~ \frac{N(N-1)}{2}~ ​ відрізків, які можна побудувати, зʼєднавши дві різні точки серед ~N~ точок. Треба побудувати M із цих відрізків.

Знайдіть кількість способів побудови ~M~ відрізків так, щоб жодні два з них не перетиналися в точці, відмінній від кінцевих. Відповідь вивести за модулем ~10^9+7~.

Обмеження

• ~1≤N≤10^7~
• ~0≤M≤ \frac{N(N-1)}{2}~ ​

Формат вхідних даних

Вхідний потік містить цілі числа ~N, M~.

Числа розділяються пропуском.

Формат вихідних даних

У вихідний потік виведіть відповідь.

Приклад вхідних даних

4 2

Приклад вихідних даних

14

Наступні приклади ліворуч і посередині задовольняють умови. (Зауважте, що допустимо, щоб відрізки перетиналися в своїх кінцевих точках.)

Приклад праворуч не підходить, оскільки два ребра перетинаються в точці, відмінній від їхніх кінцевих точок.

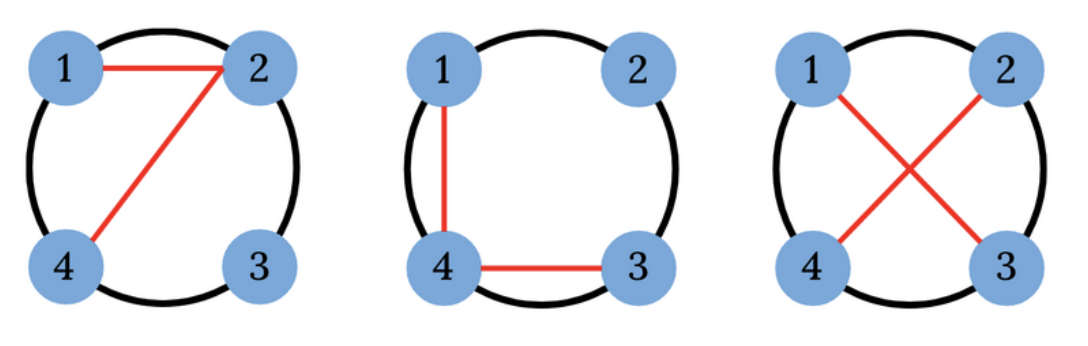
Приклад вхідних даних

6 3

Приклад вихідних даних

295

Приклад вхідних даних

2023 1217

Приклад вихідних даних

10811951