Потоколяндія - це величезна країна з ~𝑁~ містами, з'єднаними ~M~ ділянками доріг, причому жодна пара міст не з'єднується більш ніж одним відрізком доріг, і кожен відрізок дороги з'єднує різні міста. Для зручності міста пронумеровані від 1 до ~𝑁~. Ділянки доріг забезпечують повне сполучення в Потоколяндії - між кожними двома містами є дорога, яка використовує ділянки дороги.

Громадяни цієї чудової країни знову перед глибоким роздумом, адже попереду чергові вибори, навіть подвійні. З огляду на майбутні вибори влада вирішила відремонтувати деякі ділянки доріг, щоб покращити сполучення між ~𝐾~ головними містами. Точніше, мета полягає в тому, щоб мати можливість подорожувати між будь-якими двома головними містами лише відремонтованими дорогами, оскільки мережа доріг Олімпії знаходиться в занедбаному стані. Ціна ремонту відома для кожної ділянки дороги.

Напишіть програму, яка, враховуючи ділянки доріг, ціни на їх ремонт і головні міста, знаходить найменшу вартість ділянок доріг, які після ремонту з'єднають головні ~𝐾~ міст, щоб ми могли дістатися від кожного головного міста до будь-якого іншого головного міста на відремонтованих ділянках доріг.

Вхідні дані

У першому рядку записані натуральні числа ~𝑁,𝐾~ і ~𝑀~ (~2 ≤ 𝐾 ≤ 𝑁 ≤ 10^5~, ~𝐾 ≤ 5~, ~1 ≤ 𝑀 ≤ 2 \times 10^5~) - кількість міст, кількість великих міст і кількість ділянок доріг.

Другий рядок містить ~𝐾~ різних натуральних числа - номери головних міст.

Наступні ~𝑀~ рядків містять по 3 цілих числа ~𝑥, 𝑦, 𝑐~, які описують ділянку дороги з двостороннім рухом між містами з номерами ~𝑥~ і ~𝑦~ з вартістю ремонту, що дорівнює ~𝑐~ (~1 ≤ 𝑐 ≤ 10^9~).

Вихідні дані

Виведіть єдине число - мінімальну загальну вартість ремонту ділянок доріг, щоб великі міста з'єднували лише відремонтовані ділянки доріг.

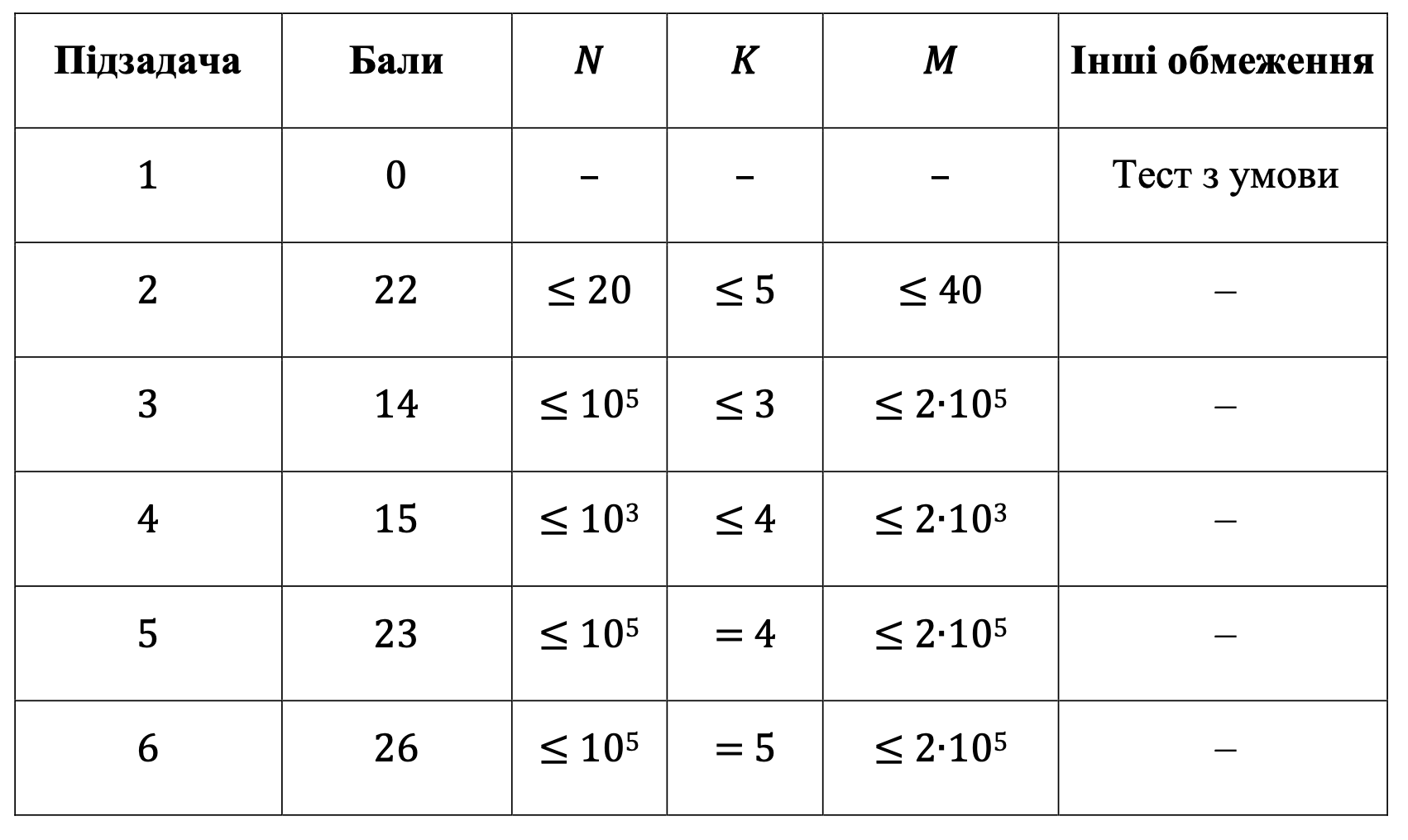
Оцінювання

Вхідні дані #1

5 3 8
5 2 3
1 2 2
2 3 3
3 4 2
4 5 5
5 1 3
3 1 3
3 5 6
4 2 2

Вихідні дані #1

8

Пояснення до прикладу:

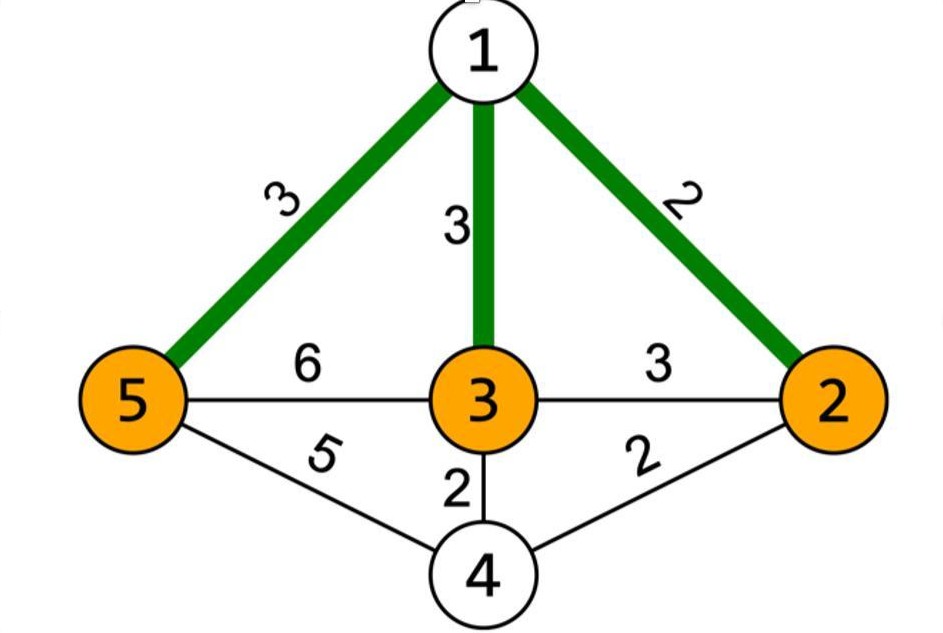
Великі міста виділені помаранчевим кольором, а оптимальні ділянки доріг для ремонту виділені жирним шрифтом і зеленим кольором. Загальна вартість їх ремонту становить 3 + 3 + 2 = 8. Вони забезпечують сполучення основних міст - у нас є дорога 5 - 1 - 3 між містами 5 і 3, дорога 5 - 1 - 2 між містами 5 і 2 і дорога 3 - 1 - 2 між містами 3 і 2.