2159: Матричка
Перегляд у форматі PDFКозак Вус готується до міжгалактичної олімпіади з інформатики, кожного дня розв'язуючи по 8 задач, і сьогодні — не виключення. Проте, дійшовши до цієї задачі, він вирішив, що йому ця задача не подобається. Саме тому тепер вирішити цю задачу повинні ви.
У вас є матриця, яка складається з ~n~ рядків та ~m~ стовпчиків. На початку усі клітини незафарбовані. Ви можете зафарбувати деяку кількість клітин в цій матриці.
Матриця буде гарною, якщо на кожній антидіагоналі є хоча б одна зафарбована клітина. Антидіагоналями називають діагоналі, що йдуть зліва знизу вправо вгору.
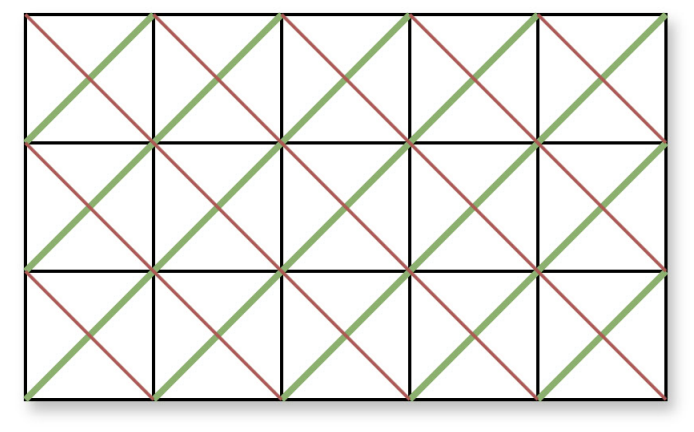
На малюнку зеленим зображені усі антидіагоналі для матриці ~n=3,m=5~, а червоним — головні діагоналі, які вас в цій задачі не цікавлять
Допоможіть Козаку Вусу і скажіть, чи можливо зафарбувати рівно ~K~ клітинок в матриці таким чином, щоб вона стала гарною.
Input
Єдиний рядок вхідних даних містить три цілі числа ~n, m, k~ (~1 \leq n, m \leq 100~; ~0 \leq k \leq n \cdot m~) — розміри матриці та кількість клітинок, яку потрібно зафарбувати відповідно.
Output
Виведіть "YES", якщо можна зафарбувати рівно ~K~ клітинок, щоб матриця стала гарною, або "NO" у іншому випадку.
Sample Input 1
3 5 7
Sample Output 1
YES
Sample Input 2
4 2 6
Sample Output 2
YES
Sample Input 3
1 1 0
Sample Output 3
NO
Sample Input 4
3 3 3
Sample Output 4
NO
Notes
У першому прикладі можна зафарбувати клітини наступним чином:
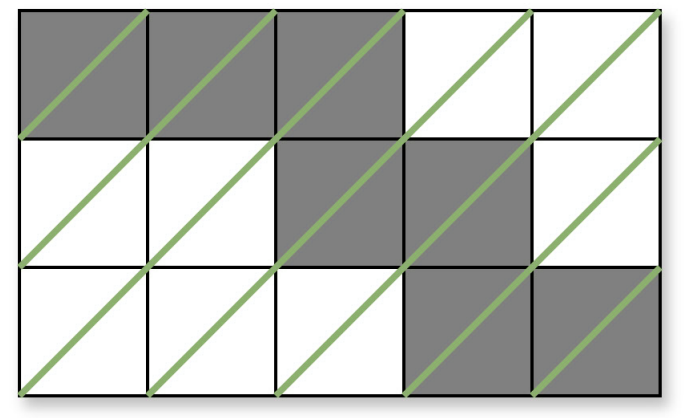
Зеленим позначено антидіагоналі, а сірим — зафарбовані клітини
У другому прикладі можна зафарбувати клітини наступним чином:
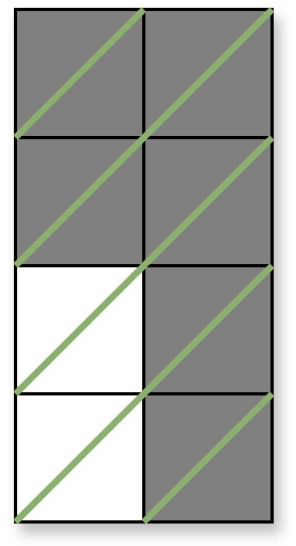
Зеленим позначено антидіагоналі, а сірим — зафарбовані клітини
У третьому та четвертому прикладах не можна зафарбувати клітини, аби матриця стала гарною.
Коментарі